（本小题满分14分）已知定义在正实数集上的函数f（x）＝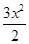
＋ax，g（x）＝4a2lnx＋b，其中a＞0，设两曲线y＝f（x）与y＝g（x）有公共点，且在公共点处的切线相同.
（1）若a＝1，求两曲线y＝f（x）与y＝g（x）在公共点处的切线方程；
（2）用a表示b，并求b的最大值.
相关试题
的前n项和为
，且
。
求数列
的前n项和
；
，
，
，
为平面四边形
的四个内角。
；
，
，
，
，
，求
的值。
的三个内角分别为
．
共线（Ⅰ）求角
的大小（Ⅱ）设角
，且满足
，试判断
的形状
是方程
的两根，求数列
通项公式（2）设
，数列
的前n项和为
,证明
．
ABC中，已知B＝45°，D是BC边上的一点，AD＝5，AC＝7，DC＝3，求AB的长．
推荐套卷
（本小题满分14分）已知定义在正实数集上的函数f（x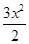）＝＋ax，g（x）＝4a2lnx＋b，其中a＞0，设两曲线y＝f（x）与y＝g（x）有公共点，且在公共点处的切线相同.
（1）若a＝1，求两曲线y＝f（x）与y＝g（x）在公共点处的切线方程；
（2）用a表示b，并求b的最大值.
粤公网安备 44130202000953号