高中数学解答题

已知某几何体的俯视图是如图所示矩形．主视图是一个底边长为8、高为4的等腰三角形，左视图是一个底边长为6、高为4的等腰三角形．

（1）判断该几何体形状；
（2）求该几何体的的体积V与侧面积S．

已知f（x）=x|x﹣a|+b，x∈R．
（1）当a=1，b=1时．f（2^x）=，求x的值；
（2）若b＜0，b为常数，任意x∈[0，1]，不等式f（x）＜0恒成立，求实数a的取值范围．

已知函数f（x）=x²﹣2ax+a+2，
（1）若f（x）≤0的解集A⊆[0，3]，求实数a的取值范围；
（2）若g（x）=f（x）+|x²﹣1|在区间（0，3）内有两个零点x₁，x₂（x₁＜x₂），求实数a的取值范围．

在△ABC中，．
（1）求的值；
（2）当△ABC的面积最大时，求∠A的大小．

某家庭进行理财投资，根据长期收益率市场预测，投资债券等稳健型产品的收益与投资额成正比，投资股票等风险型产品的收益与投资额的算术平方根成正比，已知投资1万元时两类产品的收益分别为0.125万元和0.5万元（如图）．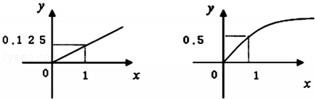

（1）分别写出两种产品的收益和投资的函数关系；
（2）该家庭现有20万元资金，全部用于理财投资，问：怎样分配资金能使投资获得最大的收益，其最大收益为多少万元？

记关于x的不等式＜0的解集为P，不等式|x﹣1|≤1的解集为Q．
（1）若a=3，求P；
（2）若a＞0，且Q⊆P，求a的取值范围．

已知定义域为R的函数是奇函数．
（Ⅰ）求a，b的值；
（Ⅱ）若对任意的t∈R，不等式f（t²﹣2t）+f（2t²﹣k）＜0恒成立，求k的取值范围．

已知函数f（x）=x²+2ax+2，x∈[﹣5，5]．
（Ⅰ）当a=﹣1时，求函数f（x）的最大值和最小值；
（Ⅱ）求实数a的取值范围，使y=f（x）在区间[﹣5，5]上是单调函数．

如图，在正方体ABCD﹣A₁B₁C₁D₁中，AA₁=2，E为AA₁的中点，O是BD₁的中点．

（Ⅰ）求证：平面A₁BD₁⊥平面ABB₁A₁；
（Ⅱ）求证：EO∥平面ABCD．

已知f（x）=2^x，g（x）是一次函数，并且点（2，2）在函数f[g（x）]的图象上，点（2，5）在函数g[f（x）]的图象上，求g（x）的解析式．

已知||=3，||=5，|+|=7．
（1）求向量与的夹角θ；
（2）当向量k+与﹣2垂直时，求实数k的值．

已知，，α，β均为锐角．
（1）求sin2α的值；
（2）求sinβ的值．

已知函数f（x）=x²﹣3x的定义域为{1，2，3}，则f（x）的值域为  ．

设二次函数f（x）=ax²+bx+c（a，b，c∈R）满足下列条件：
①当x∈R时，f（x）的最小值为0，且f（x﹣1）=f（﹣x﹣1）恒成立；
②当x∈（0，5）时，x≤f（x）≤2|x﹣1|+1恒成立．
（1）求f（1）的值；
（2）求f（x）的解析式；
（3）求最大的实数m（m＞1），使得存在实数t，只要当x∈[1，m]时，就有f（x+t）≤x成立．

化简下列各式（写出化简过程）
（1）；
（2）lg5•lg20+lg²2．