江苏省常州市溧阳市高一上学期期末数学试卷
已知函数f(x)=3sin(ωx+φ)(ω>0,0≤φ<π)的部分图象如图所示,则该函数的解析式为f(x)= .
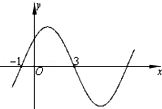
来源:2015-2016学年江苏省常州市溧阳市高一上学期期末数学试卷
在平行四边形ABCD中,E为BC的中点,F在线段DC上,且CF=2DF.若 ,λ,μ均为实数,则λ+μ的值为 .
,λ,μ均为实数,则λ+μ的值为 .
来源:2015-2016学年江苏省常州市溧阳市高一上学期期末数学试卷
已知f(x)是定义在R上且周期为6的奇函数,当x∈(0,3)时,f(x)=lg(2x2﹣x+m).若函数f(x)在区间[﹣3,3]上有且仅有5个零点(互不相同),则实数m的取值范围是 .
来源:2015-2016学年江苏省常州市溧阳市高一上学期期末数学试卷
对任意两个非零的平面向量 ,
, ,定义
,定义 和
和 之间的新运算⊙:
之间的新运算⊙: .已知非零的平面向量
.已知非零的平面向量 满足:
满足: 和
和 都在集合
都在集合 中,且
中,且 .设
.设 与
与 的夹角
的夹角 ,则
,则 = .
= .
来源:2015-2016学年江苏省常州市溧阳市高一上学期期末数学试卷
已知| |=3,|
|=3,| |=5,|
|=5,| +
+ |=7.
|=7.
(1)求向量 与
与 的夹角θ;
的夹角θ;
(2)当向量k +
+ 与
与 ﹣2
﹣2 垂直时,求实数k的值.
垂直时,求实数k的值.
来源:2015-2016学年江苏省常州市溧阳市高一上学期期末数学试卷
某食品的保鲜时间y(单位:小时)与储存温度x(单位:℃)之间满足函数关系y=ekx+b(e=2.718为自然对数的底数,k,b为常数).已知该食品在0℃的保鲜时间为160小时,在20℃的保鲜时间为40小时.
(1)求该食品在30℃的保鲜时间;
(2)若要使该食品的保鲜时间至少为80小时,则储存温度需要满足什么条件?
来源:2015-2016学年江苏省常州市溧阳市高一上学期期末数学试卷
已知函数f(x)=4﹣log2x,g(x)=log2x.
(1)当 时,求函数h(x)=f(x)•g(x)的值域;
时,求函数h(x)=f(x)•g(x)的值域;
(2)若对任意的x∈[1,8],不等式f(x3)•f(x2)>kg(x)恒成立,求实数k的取值范围.
来源:2015-2016学年江苏省常州市溧阳市高一上学期期末数学试卷
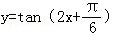 的最小正周期为 .
的最小正周期为 . =(1,2),
=(1,2), =(﹣2,2),则|
=(﹣2,2),则| )=2,则tanα= .
)=2,则tanα= . ,则sin4α﹣cos4α= .
,则sin4α﹣cos4α= . cosα=m﹣1,则实数m的取值范围是 .
cosα=m﹣1,则实数m的取值范围是 . ,
, ,α,β均为锐角.
,α,β均为锐角. ,
, ,θ为第二象限角.
,θ为第二象限角. ,求sinθ﹣cosθ的值;
,求sinθ﹣cosθ的值; ∥
∥ ,求
,求 的值.
的值. .
. 的值;②求
的值;②求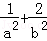 的取值范围;
的取值范围; 粤公网安备 44130202000953号
粤公网安备 44130202000953号