[选修4-1:几何证明选讲]如图,⊙O中 的中点为P,弦PC,PD分别交AB于E,F两点.
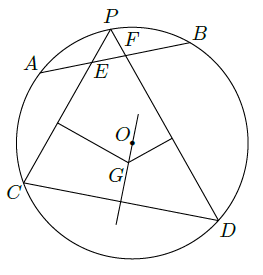
(1)若 ,求 的大小;
(2)若EC的垂直平分线与FD的垂直平分线交于点G,证明: .
设函数 .
(1)讨论 的单调性;
(2)证明当x∈(1,+∞)时,1< <x;
(3)设c>1,证明当x∈(0,1)时,1+(c﹣1)x>cx .
已知抛物线 的焦点为F,平行于x轴的两条直线 , 分别交C于A,B两点,交C的准线于P,Q两点.
(1)若F在线段AB上,R是PQ的中点,证明 ;
(2)若 的面积是 的面积的两倍,求AB中点的轨迹方程.
如图,四棱锥 中, , , , ,M为线段AD上一点, ,N为PC的中点.
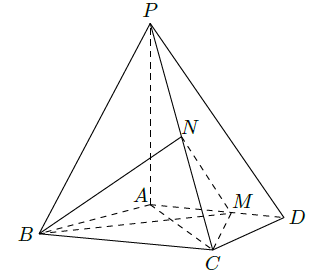
(1)证明 ;
(2)求四面体 的体积.
如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
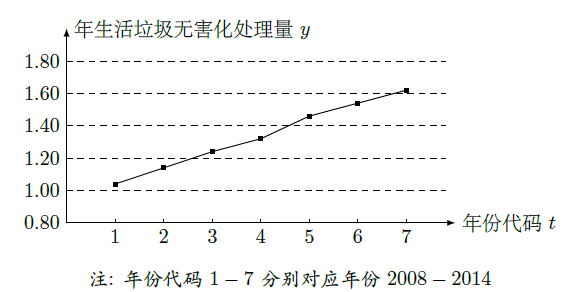
(1)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以证明;
(2)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据: , , , .
参考公式: ,回归方程 中斜率和截距的最小二乘估计公式分别为:
, .
在平面直角坐标系xOy中,已知椭圆Γ: ,A为Γ的上顶点,P为Γ上异于上、下顶点的动点,M为x正半轴上的动点.
(1)若P在第一象限,且|OP|= ,求P的坐标;
(2)设P ,若以A、P、M为顶点的三角形是直角三角形,求M的横坐标;
(3)若 ,直线AQ与Γ交于另一点C,且 , ,求直线AQ的方程.
根据预测,某地第n(n∈N *)个月共享单车的投放量和损失量分别为 和 (单位:辆),其中 , ,第n个月底的共享单车的保有量是前n个月的累计投放量与累计损失量的差.
(1)求该地区第4个月底的共享单车的保有量;
(2)已知该地共享单车停放点第n个月底的单车容纳量 (单位:辆).设在某月底,共享单车保有量达到最大,问该保有量是否超出了此时停放点的单车容纳量?
已知函数 .
(1)求 的单调递增区间;
(2)设△ABC为锐角三角形,角A所对边 ,角B所对边b=5,若 ,求△ABC的面积.
如图,直三棱柱ABC﹣A 1B 1C 1的底面为直角三角形,两直角边AB和AC的长分别为4和2,侧棱 的长为5.

(1)求三棱柱ABC﹣A 1B 1C 1的体积;
(2)设M是BC中点,求直线A 1M与平面ABC所成角的大小.
记 分别为函数 的导函数.若存在 ,满足 且 ,则称 为函数 与 的一个“S点”.
(1)证明:函数 与 不存在“S点”.
(2)若函数 与 存在“S点”,求实数 的值.
(3)已知函数 , ,对任意 ,判断是否存在 ,使函数 与 在区间 内存在“S”点,并说明理由.
如图,在平面直角坐标系 中,椭圆C过点 ,焦点 ,圆O的直径为 .

(1)求椭圆C及圆O的方程;
(2)设直线 与圆O相切于第一象限内的点P.
①若直线 与椭圆C有且只有一个公共点,求点P的坐标;
②直线 与椭圆C交于A、B两点.若 的面积为 ,求直线 的方程.
某农场有一块农田,如图所示,它的边界由圆 的一段圆弧 ( 为此圆弧的中点)和线段 构成,已知圆 的半径为40米,点 到 的距离为50米,先规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形 .大棚Ⅱ内的地块形状为 要求 均在线段 上, 均在圆弧上,设 与 所成的角为
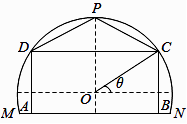
(1)用 分别表示矩形 和 的面积,并确定 的取值范围
(2)若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为 .求当 为何值时,能使甲、乙两种蔬菜的年总产值最大.