已知函数 f( x)=﹣ x 2+ ax+4, g( x)=| x+1|+| x﹣1|.
(1)当 a=1时,求不等式 f( x)≥ g( x)的解集;
(2)若不等式 f( x)≥ g( x)的解集包含[﹣1,1],求 a的取值范围.
在直角坐标系 xOy中,曲线 C的参数方程为 ,(θ为参数),直线 l的参数方程为 ,( t为参数).
(1)若 a=﹣1,求 C与 l的交点坐标;
(2)若 C上的点到 l距离的最大值为 ,求 a.
设 A, B为曲线 C: y 上两点, A与 B的横坐标之和为4.
(1)求直线 AB的斜率;
(2)设 M为曲线 C上一点, C在 M处的切线与直线 AB平行,且 AM⊥ BM,求直线 AB的方程.
为了监控某种零件的一条生产线的生产过程,检验员每隔30 min从该生产线上随机抽取一个零件,并测量其尺寸(单位: cm).下面是检验员在一天内依次抽取的16个零件的尺寸:
| 抽取次序 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 零件尺寸 |
9.95 |
10.12 |
9.96 |
9.96 |
10.01 |
9.92 |
9.98 |
10.04 |
| 抽取次序 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| 零件尺寸 |
10.26 |
9.91 |
10.13 |
10.02 |
9.22 |
10.04 |
10.05 |
9.95 |
经计算得 x i=9.97, s 0.212, 18.439, ( x i )( i﹣8.5)=﹣2.78,其中 x i为抽取的第 i个零件的尺寸, i=1,2,…,16.
(1)求( x i, i)( i=1,2,…,16)的相关系数 r,并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小(若| r|<0.25,则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小).
(2)一天内抽检零件中,如果出现了尺寸在( 3 s, 3 s)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)从这一天抽检的结果看,是否需对当天的生产过程进行检查?
(ⅱ)在( 3 s, 3 s)之外的数据称为离群值,试剔除离群值,估计这条生产线当天生产的零件尺寸的均值与标准差.(精确到0.01)
附:样本( x i, y i)( i=1,2,…, n)的相关系数 r , 0.09.
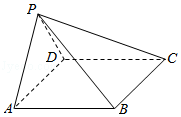
如图,在四棱锥 P﹣ ABCD中, AB∥ CD,且∠ BAP=∠ CDP=90°.
(1)证明:平面 PAB⊥平面 PAD;
(2)若 PA= PD= AB= DC,∠ APD=90°,且四棱锥 P﹣ ABCD的体积为 ,求该四棱锥的侧面积.
记 S n为等比数列{ a n}的前 n项和.已知 S 2=2, S 3=﹣6.
(1)求{ a n}的通项公式;
(2)求 S n,并判断 S n +1, S n, S n +2是否成等差数列.
设 O为坐标原点,动点 M在椭圆 C: y 2=1上,过 M作 x轴的垂线,垂足为 N,点 P满足 .
(1)求点 P的轨迹方程;
(2)设点 Q在直线 x=﹣3上,且 • 1.证明:过点 P且垂直于 OQ的直线 l过 C的左焦点 F.
海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位: kg),其频率分布直方图如下:
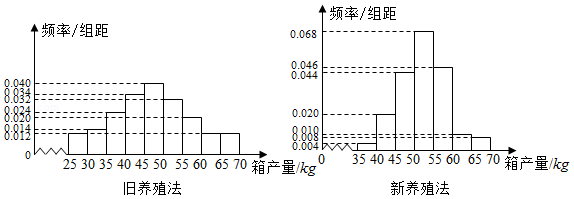
(1)记 A表示事件"旧养殖法的箱产量低于50 kg",估计 A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
| |
箱产量<50 kg |
箱产量≥50 kg |
| 旧养殖法 |
|
|
| 新养殖法 |
|
|
(3)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行比较.
附:
| P( K 2≥ K) |
0.050 |
0.010 |
0.001 |
| K |
3.841 |
6.635 |
10.828 |
K 2 .
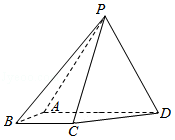
如图,四棱锥 P﹣ ABCD中,侧面 PAD为等边三角形且垂直于底面 ABCD, AB= BC AD,∠ BAD=∠ ABC=90°.
(1)证明:直线 BC∥平面 PAD;
(2)若△ PCD面积为2 ,求四棱锥 P﹣ ABCD的体积.
已知等差数列{ a n}的前 n项和为 S n,等比数列{ b n}的前 n项和为 T n, a 1=﹣1, b 1=1, a 2+ b 2=2.
(1)若 a 3+ b 3=5,求{ b n}的通项公式;
(2)若 T 3=21,求 S 3.
[选修4―4:坐标系与参数方程]
在直角坐标系 中,曲线 C的参数方程为 ,直线 l的参数方程为 .
(1)若 ,求 C与 l的交点坐标;
(2)若 C上的点到 l的距离的最大值为 ,求a.
已知椭圆C: ,四点P1(1,1),P2(0,1),P3 ,P4 中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布 .
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在 之外的零件数,求 及 的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
9.95 |
10.12 |
9.96 |
9.96 |
10.01 |
9.92 |
9.98 |
10.04 |
10.26 |
9.91 |
10.13 |
10.02 |
9.22 |
10.04 |
10.05 |
9.95 |
经计算得
,
,其中
为抽取的第
 个零件的尺寸,
.
个零件的尺寸,
.
用样本平均数 作为 的估计值 ,用样本标准差 作为 的估计值 ,利用估计值判断是否需对当天的生产过程进行检查?剔除 之外的数据,用剩下的数据估计 和 (精确到0.01).
附:若随机变量 服从正态分布 ,则 ,
, .
如图,在四棱锥 中, ,且 .
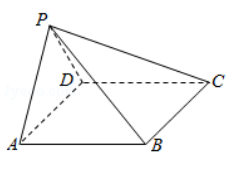
(1)证明:平面 平面 ;
(2)若 , ,求二面角 的余弦值.