已知圆C: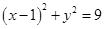 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线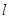 交圆C于A、B两点.
交圆C于A、B两点.
(1)当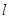 经过圆心C时,求直线l的方程;
经过圆心C时,求直线l的方程;
(2)当弦AB最短时,写出直线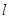 的方程;
的方程;
(3)当直线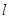 的倾斜角为45º时,求弦AB的长.
的倾斜角为45º时,求弦AB的长.
已知函数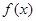 是定义在R上的偶函数,且当
是定义在R上的偶函数,且当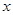 ≤0时,
≤0时,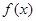
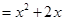 .
.
(1)现已画出函数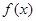 在y轴左侧的图像,如图所示,请补出完整函数
在y轴左侧的图像,如图所示,请补出完整函数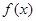 的图像,并根据图像写出函数
的图像,并根据图像写出函数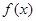 的增区间;
的增区间; 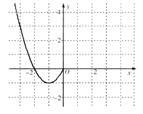
(2)写出函数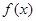 的解析式和值域.
的解析式和值域.
已知f(x)是二次函数,不等式f(x)<0的解集是(0,5) ,且f(x)在区间[-1,4]上的最大值是12.
(1)求f(x)的解析式.
(2)求f(x)在区间[-1,4]的值域.
已知数列{an}满足的前n项和为Sn,且Sn= +n﹣1,(n∈N*).
+n﹣1,(n∈N*).
(1)求数列{an}的通项公式;
(2)若数列{bn}的通项公式满足bn=n(1﹣an),求数列{bn}的前n项和Tn.
已知10件不同产品中有4件是次品,现对它们进行一一测试,直至找出所有4件次品为止.
(1)若恰在第5次测试,才测试到第一件次品,第十次才找到最后一件次品,则这样的不同测试方法数是多少?
(2)若恰在第5次测试后,就找出了所有4件次品,则这样的不同测试方法数是多少?
如图,在平面直角坐标系xOy中,已知椭圆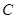 :
: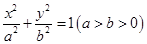 的
的
离心率为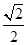 ,且右焦点F到左准线l的距离为
,且右焦点F到左准线l的距离为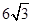 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)(1)设椭圆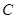 上的任一点
上的任一点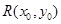 ,从原点
,从原点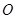 向圆
向圆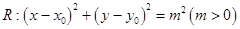 引两条
引两条
切线,设两条切线的斜率分别为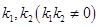 ,当
,当 为定值时求
为定值时求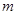 的值;
的值;
(2)在(1)的条件下,当两条切线分别交椭圆于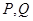 时,试探究
时,试探究 是否为定值,若是,求出其值;若不是,请说明理由.
是否为定值,若是,求出其值;若不是,请说明理由.
如图,四棱锥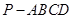 中,侧面
中,侧面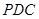 是边长为2的正三角形,底面
是边长为2的正三角形,底面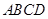 是菱形,
是菱形,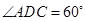 ,点
,点 在底面
在底面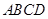 上的射影为
上的射影为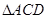 的重心,点
的重心,点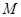 为线段
为线段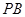 上的点.
上的点.
(1)当点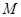 为
为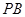 的中点时,求证:
的中点时,求证: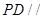 平面
平面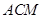 ;
;
(2)当平面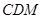 与平面
与平面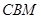 所成锐二面角的余弦值为
所成锐二面角的余弦值为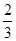 时,求
时,求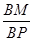 的值.
的值.
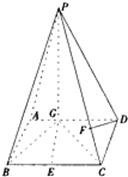
如图,四棱锥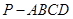 中,底面
中,底面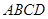 是平行四边形,
是平行四边形,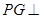 平面
平面 ,垂足为
,垂足为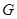 ,
,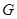 在线段
在线段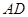 上,
上,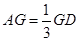 ,
,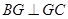 ,
,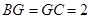 ,
,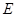 是
是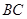 的中点,四面体
的中点,四面体 的体积为
的体积为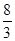 .
.
(1)求异面直线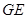 与
与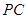 所成角的余弦值;
所成角的余弦值;
(2)棱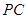 上是否存在一点
上是否存在一点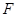 ,使
,使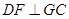 ,若存在,求
,若存在,求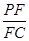 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.