四棱锥P-ABCD中,底面ABCD是正方形,边长为a,PD=a,PA=PC=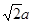 ,
,
(1)求证:PD⊥平面ABCD;
(2)求证,直线PB与AC垂直;
选修4—1:几何证明选讲.
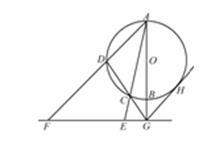
如图,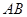 是圆
是圆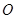 的直径,
的直径,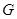 是
是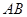 延长线上的一点,
延长线上的一点,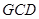 是圆
是圆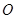 的割线,过点
的割线,过点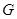 作
作 的垂线,交直线
的垂线,交直线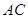 于点
于点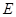 ,交直线
,交直线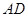 于点
于点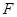 ,过点
,过点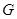 作圆
作圆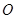 的切线,切点为
的切线,切点为 .
.
(1)求证: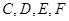 四点共圆;
四点共圆;
(2)若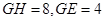 ,求
,求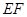 的长.
的长.
已知等比数列 的首项
的首项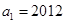 ,公比
,公比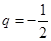 ,数列
,数列 前n项和记为
前n项和记为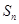 ,前n项积记为
,前n项积记为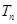 .
.
(1)证明: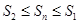 ;
;
(2)求n为何值时,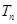 取得最大值;
取得最大值;
(3)证明:若数列 中的任意相邻三项按从小到大排列,则总可以使其成等差数列;若所有这些等差数列的公差按从大到小的顺序依次记为
中的任意相邻三项按从小到大排列,则总可以使其成等差数列;若所有这些等差数列的公差按从大到小的顺序依次记为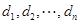 ,则数列
,则数列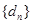 为等比数列.
为等比数列.
已知等差数列{an}满足a2=2,a5=8.
(1)求{an}的通项公式;
(2)各项均为正数的等比数列{bn}中,b1=1,b2+b3=a4,求{bn}的前n项和Tn.
(本小题满分12分)已知圆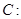
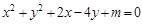 与
与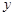 轴相切.
轴相切.
(1)求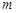 的值;
的值;
(2)若圆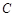 的切线在
的切线在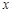 轴和
轴和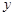 轴上的截距相等,求该切线方程;
轴上的截距相等,求该切线方程;
(3)从圆外一点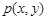 向圆引切线,M为切点,O为坐标原点,且有
向圆引切线,M为切点,O为坐标原点,且有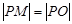 ,求使
,求使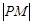 最小的点P的坐标.
最小的点P的坐标.
(本小题10分)已知圆心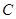 的坐标为(1,1),圆
的坐标为(1,1),圆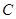 与
与 轴和
轴和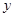 轴都相切.
轴都相切.
(1)求圆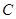 的方程;
的方程;
(2)求与圆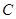 相切,且在
相切,且在 轴和
轴和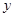 轴上的截距相等的直线方程.
轴上的截距相等的直线方程.