(满分14分)已知定义在正实数集上的函数 ,
, ,其中
,其中 .
.
设两曲线 ,
, 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(1)用 表示
表示 ;
;
(2)试证明不等式: (
( ).
).
已知函数
 .
.
(1)讨论函数 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(2)若函数 在
在 处取得极值,对
处取得极值,对
 ,
, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当 且
且 时,试比较
时,试比较 的大小
的大小
(本小题满分12分)
已知函数 且导数
且导数 .
.
(1)试用含有 的式子表示
的式子表示 ,并求
,并求 的单调区间;
的单调区间;
(2)对于函数图象上不同的两点 ,且
,且 ,如果在函数图像上存在点
,如果在函数图像上存在点 (其中
(其中 )使得点
)使得点 处的切线
处的切线 ,则称
,则称 存在“相依切线”.特别地,当
存在“相依切线”.特别地,当 时,又称
时,又称 存在“中值相依切线”.试问:在函数
存在“中值相依切线”.试问:在函数 上是否存在两点
上是否存在两点 使得它存在“中值相依切线”?若存在,求
使得它存在“中值相依切线”?若存在,求 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
已知函数 ,其中
,其中 .
.
(Ⅰ)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求f(x)的单调区间.
已知函数
 为自然对数的底数).
为自然对数的底数).
(1)求曲线 在
在 处的切线方程;
处的切线方程;
(2)若 是
是 的一个极值点,且点
的一个极值点,且点 ,
, 满足条件:
满足条件: .
.
(ⅰ)求 的值;
的值;
(ⅱ)求证:点 ,
, ,
, 是三个不同的点,且构成直角三角形.
是三个不同的点,且构成直角三角形.
(本小题满分14分)已知函数 ,
, 是常数.
是常数.
(Ⅰ) 证明曲线 在点
在点 的切线经过
的切线经过 轴上一个定点;
轴上一个定点;
(Ⅱ) 若 对
对 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(参考公式: )
)
(Ⅲ)讨论函数 的单调区间.
的单调区间.
已知 ,函数
,函数 ,
, (其中
(其中 为自然对数的底数).
为自然对数的底数).
(Ⅰ)判断函数 在
在 上的单调性;
上的单调性;
(II)是否存在实数 ,使曲线
,使曲线 在点
在点 处的切线与
处的切线与 轴垂直? 若存在,
轴垂直? 若存在,
求出 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅲ)若实数 满足
满足 ,求证:
,求证: .
.
已知函数 ,
, ,函数
,函数 的图象在点
的图象在点 处的切线平行于
处的切线平行于 轴.
轴.
(1)确定 与
与 的关系;
的关系;
(2)试讨论函数 的单调性;
的单调性;
(3)证明:对任意 ,都有
,都有 成立。
成立。
(本小题满分14分)已知函数
(1)若在 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值;
(2)若 在区间(-2,3)内有两个不同的极值点,求a 取值范围;
在区间(-2,3)内有两个不同的极值点,求a 取值范围;
(3)在(1)的条件下,是否存在实数m,使得函数 的图象与函数
的图象与函数 的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
已知函数 (其中
(其中 ,
, ),函数
),函数 的导函数为
的导函数为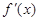 ,且
,且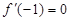 .
.
(Ⅰ)若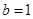 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若函数 在区间
在区间 上的最小值为
上的最小值为 ,求
,求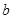 的值.
的值.
已知函数f (x)=lnx,g(x)=ex.
(I)若函数φ (x) = f (x)- ,求函数φ (x)的单调区间;
,求函数φ (x)的单调区间;
(Ⅱ)设直线l为函数的图象上一点A(x0,f (x0))处的切线.证明:在区间(1,+∞)上存在唯一的x0,使得直线l与曲线y=g(x)相切.