(本小题满分12分)
已知函数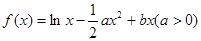 且导数
且导数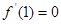 .
.
(1)试用含有 的式子表示
的式子表示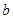 ,并求
,并求 的单调区间;
的单调区间;
(2)对于函数图象上不同的两点 ,且
,且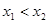 ,如果在函数图像上存在点
,如果在函数图像上存在点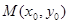 (其中
(其中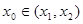 )使得点
)使得点 处的切线
处的切线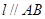 ,则称
,则称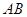 存在“相依切线”.特别地,当
存在“相依切线”.特别地,当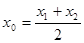 时,又称
时,又称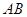 存在“中值相依切线”.试问:在函数
存在“中值相依切线”.试问:在函数 上是否存在两点
上是否存在两点 使得它存在“中值相依切线”?若存在,求
使得它存在“中值相依切线”?若存在,求 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
相关知识点
推荐套卷
(本小题满分12分)
已知函数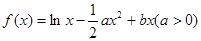 且导数
且导数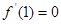 .
.
(1)试用含有 的式子表示
的式子表示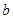 ,并求
,并求 的单调区间;
的单调区间;
(2)对于函数图象上不同的两点 ,且
,且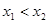 ,如果在函数图像上存在点
,如果在函数图像上存在点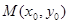 (其中
(其中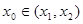 )使得点
)使得点 处的切线
处的切线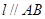 ,则称
,则称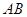 存在“相依切线”.特别地,当
存在“相依切线”.特别地,当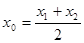 时,又称
时,又称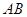 存在“中值相依切线”.试问:在函数
存在“中值相依切线”.试问:在函数 上是否存在两点
上是否存在两点 使得它存在“中值相依切线”?若存在,求
使得它存在“中值相依切线”?若存在,求 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.