高中数学组合几何解答题

已知函数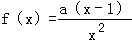，其中a＞0．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）若直线x﹣y﹣1=0是曲线y=f（x）的切线，求实数a的值；
（Ⅲ）设g（x）=xlnx﹣x²f（x），求g（x）在区间[1，e]上的最小值．（其中e为自然对数的底数）

已知函数，其中.
（1）求函数的单调区间；
（2）若直线是曲线的切线，求实数的值；
（3）设，求在区间上的最大值.（其中为自然对数的底数）

已知函数
（1）求曲线在点处的切线的方程；
（2）直线为曲线的切线，且经过原点，求直线的方程及切点的坐标；
（3）如果曲线的某一切与直线垂直，求切点坐标和切线方程。

设函数
(I) 讨论的单调性；
（II）若有两个极值点和，记过点的直线的斜率为，问：是否存在，使得？若存在，求出的值，若不存在，请说明理由．
参考答案

（本小题满分14分）已知函数
（I）若曲线在点处的切线与直线垂直，求a的值；
（II）若在区间单调递增，求a的取值范围；
（III）若—1＜a＜3，证明：对任意都有＞1成立.

已知函数，其中．
（1）当时，求曲线在原点处的切线方程；
（2）求的单调区间.

(本题满分14分) 已知
（Ⅰ）当时，求曲线在点处的切线方程；
（Ⅱ）若在处有极值，求的单调递增区间；
（Ⅲ）是否存在实数，使在区间的最小值是3，若存在，求出的值；
若不存在，说明理由.

已知函数.
（1）求在点处的切线方程；
（2）求函数在上的最大值.

（本小题满分15分）
已知函数其中e为自然对数的底数。
（I）若函数f (x)在[1, 2]上为单调增函数，求实数a的取值范围；
（II）设曲线y=" f" (x)在点P(1, f (1))处的切线为l .试问：是否存在正实数a ，使得函数y=" f" (x)的图象被点P 分割成的两部分（除点P 外）完全位于切线l 的两侧？若存在，请求出a 满足的条件，若不存在，请说明理由.

在F1赛车中，赛车位移与比赛时间t存在函数关系s＝10t＋5t²(s的单位为m，t的单位为s)．求：
(1)t＝20s，Δt＝0.1s时的Δs与；
(2)t＝20s时的瞬时速度．

（本小题满分12分）已知函数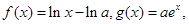其中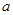为常数，函数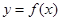和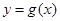的图象在它们与坐标轴交点的切线互相平行．
（1）求函数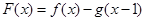的单调区间；
（2）若不等式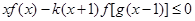在区间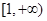上恒成立，求实数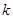的取值范围．

已知函数.
（1）求在点处的切线方程；
（2）求函数在上的最大值.

设f(x)＝x＋ax²＋bln x，曲线y＝f(x)过点
P(1,0)，且在P点处的切线的斜率为2.
①求a，b的值；
②证明：f(x)≤2x－2.

设函数，
（1）若函数在处与直线相切；
①求实数，的值；②求函数上的最大值；
（2）当时，若不等式对所有的，都成立，求实数的取值范围．

己知函数，其中 
（1）求函数的单调区间；
（2）若直线x-y-l=0是曲线y=的切线，求实数的值；
（3）设，求g（x）在区间上的最大值（其中e为自然对数的底数）