[山东]2012届山东省威海市高三第一次模拟考试理科数学试卷
设集合 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分又不必要条件 |
在一次数学测验中,统计7名学生的成绩分布茎叶如右图所示,若这7名学生的平均成绩为77分,则x的值为
| A.5 | B.6 | C.7 | D.8 |
设 为三条不同的直线,
为三条不同的直线, 为两个不同的平面,下列命题中正确的是( )
为两个不同的平面,下列命题中正确的是( )
A.若 则 则 |
B.若 则 则 |
C.若 则 则 |
D.若 则 则 |
已知圆的方程为 设该圆中过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积是
设该圆中过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积是
A. |
B. |
C. |
D. |
甲乙两人进行跳绳比赛,规定:若甲赢一局,比赛结束,甲胜出;若乙赢两局,比赛结束,乙胜出.已知每一局甲、乙二人获胜的概率分别为 、
、 ,则甲胜出的概率为
,则甲胜出的概率为
A. |
B. |
C. |
D. |
函数 的图象如右图所示,下列说法正确的是( )
的图象如右图所示,下列说法正确的是( )
①函数 满足
满足
②函数 满足
满足
③函数 满足
满足
④函数 满足
满足
| A.①③ | B.②④ | C.①② | D.③④ |
下列四种说法
①命题 “ >0”的否定是“
>0”的否定是“ ”;
”;
②“命题 为真”是“命题
为真”是“命题 为真”的必要不充分条件;
为真”的必要不充分条件;
③“若 <
< ,则
,则 <
< ”的逆命题为真;
”的逆命题为真;
④若实数 ,则满足:
,则满足: >1的概率为
>1的概率为 ;
;
正确的有___________________.(填序号)
(本小题满分12分)
已知向量 且满足
且满足
(I)求函数 的单调递增区间;
的单调递增区间;
(II)设 的内角A满足
的内角A满足 且
且 ,求边BC的最小值.
,求边BC的最小值.
(本小题满分12分)设 是单调递增的等差数列,
是单调递增的等差数列, 为其前n项和,且满足
为其前n项和,且满足 是
是 的等比中项.
的等比中项.
(I)求数列 的通项公式;
的通项公式;
(II)是否存在 ,使
,使 ?说明理由;
?说明理由;
(III)若数列 满足
满足 求数列
求数列 的通项公式.
的通项公式.
(本小题满分12分)如图三棱柱 中,底面
中,底面 侧面
侧面 为等边三角形,
为等边三角形, 且AB=BC,三棱锥
且AB=BC,三棱锥 的体积为
的体积为

(I)求证: ;
;
(II)求直线 与平面BAA1所成角的正弦值.
与平面BAA1所成角的正弦值.
(本小题满分12分)现有正整数1,2,3,4,5,…n,一质点从第一个数1出发顺次跳动,质点的跳动步数通过抛掷骰子来决定:骰子的点数小于等于4时,质点向前跳一步;骰子的 点数大于
点数大于 4时,质点向前跳两步.
4时,质点向前跳两步.
(I)若抛掷骰子二次, 质点到达的正整数记为
质点到达的正整数记为 ,求E
,求E ;
;
(II)求质点恰好到达正整数5的概率.
(本小题满分12分)已知椭圆 (0<b<2)的离心率等于
(0<b<2)的离心率等于 抛物线
抛物线 (p>0).
(p>0).
(1)若抛物线的焦点F在椭圆的顶点上,求椭圆和抛物线的方程;
(II)若抛物 线的焦点F为
线的焦点F为 ,在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足
,在抛物线上是否存在点P,使得过点P的切线与椭圆相交于A,B两点,且满足 ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.
 则
则




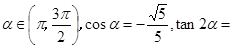
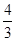
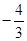
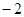
 中,已知对任意
中,已知对任意 …
… 则
则 …
… 等于
等于



 ,则二项式
,则二项式 的展开式的常数项是( )
的展开式的常数项是( )

 则
则 的值为
的值为 B、
B、 C、
C、 D、
D、
 在R上单调递增,设
在R上单调递增,设 ,若有
,若有 ,则
,则 的取值范围是( )
的取值范围是( )




 满足
满足 ,则
,则 的最大值为__________.
的最大值为__________. ,则不等式
,则不等式 的解集是_________.
的解集是_________.
 在点
在点 处的切线与直线
处的切线与直线 垂直,求a的值;
垂直,求a的值; 单调递增,求a的取值范围;
单调递增,求a的取值范围; 1<a<3,证明:对任意
1<a<3,证明:对任意 都有
都有 >1成立.
>1成立. 粤公网安备 44130202000953号
粤公网安备 44130202000953号