已知函数 (
( ),相邻两对称轴之间的距离为
),相邻两对称轴之间的距离为 .
.
(1)求函数 的解析式;
的解析式;
(2)把函数 的图象向右平移
的图象向右平移 个单位,再纵坐标不变横坐标缩短到原来的
个单位,再纵坐标不变横坐标缩短到原来的 后得到函数
后得到函数 的图象,当
的图象,当 时,求函数
时,求函数 的单调递增区间.
的单调递增区间.
已知命题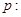
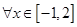 ,函数
,函数 的值大于
的值大于 .若
.若 是真命题,则命题
是真命题,则命题 可以是( )
可以是( )
A.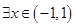 ,使得 ,使得 |
B.“ ”是“函数 ”是“函数 在区间 在区间 上有零点”的必要不充分条件 上有零点”的必要不充分条件 |
C.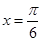 是曲线 是曲线 的一条对称轴 的一条对称轴 |
D.若 ,则在曲线 ,则在曲线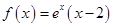 上任意一点处的切线的斜率不小于 上任意一点处的切线的斜率不小于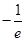 |
函数 的图象如下图所示,为了得到
的图象如下图所示,为了得到 的图像,可以将
的图像,可以将 的图像 ( )
的图像 ( )

A.向右平移 个单位长度 个单位长度 |
B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 |
D.向左平移 个单位长度 个单位长度 |
已知函数f(x)=sinx+cosx.
(1)若f(x)=2f(﹣x),求 的值;
的值;
(2)求函数F(x)=f(x)•f(﹣x)+f2(x)的最大值和单调递增区间.
(本小题满分13分)函数y=Asin(ωx+ )(A>0,ω>0)在x∈(0,7π)内取到一个最大值和一个最小值,且当x=
)(A>0,ω>0)在x∈(0,7π)内取到一个最大值和一个最小值,且当x=
π时,y有最大值3,当x=6π时,y有最小值-3.
(1)求此函数解析式;
(2)写出该函数的单调递增区间;
(3)是否存在实数m,满足不等式Asin( )>Asin(
)>Asin( )?若存在,求出m值(或范围),若不存在,请说明理由.
)?若存在,求出m值(或范围),若不存在,请说明理由.
已知函数f(x)=2sinωxcosωx﹣2 sin2ωx+
sin2ωx+ (ω>0),直线x=x1,x=x2是函数y=f(x)的图象的任意两条对称轴,且|x1﹣x2|的最小值为
(ω>0),直线x=x1,x=x2是函数y=f(x)的图象的任意两条对称轴,且|x1﹣x2|的最小值为 .
.
(Ⅰ)求ω的值;
(Ⅱ)求函数f(x)的单调增区间;
(Ⅲ)若f(α)= ,求sin(
,求sin( π﹣4α)的值.
π﹣4α)的值.
已知函数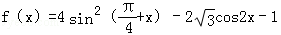 ,且给定条件p:“
,且给定条件p:“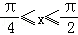 ”,
”,
(1)求f(x)的最大值及最小值
(2)若又给条件q:“|f(x)﹣m|<2“且p是q的充分条件,求实数m的取值范围.
(本小题满分12分)已知函数f (x)=Asin(ωx+φ) (A>0,ω>0,|φ|< )在一个周期内的图象如图所示.
)在一个周期内的图象如图所示.
(1)求函数的解析式;
(2)设0<x<π,且方程f (x)=m有两个不同的实数根,求实数m的取值范围以及这两个根的和.
已知函数 (其中
(其中 为常数,且
为常数,且 )的部分图像如图所示.
)的部分图像如图所示.
(1)求函数 的解析式
的解析式
(2)若 求
求 的值
的值
设函数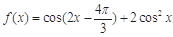 ,
,
(Ⅰ)求 的最大值,并写出使
的最大值,并写出使 取最大值时x的集合;
取最大值时x的集合;
(Ⅱ)已知 中,角A、B、C的对边分别为a、b、c,若
中,角A、B、C的对边分别为a、b、c,若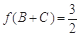 ,
, ,求
,求 的面积的最大值.
的面积的最大值.