高中数学多面角及多面角的性质试题

函数的最小正周期是（ ）

A．4π

B．2π

C．π

D．

设函数
（Ⅰ）当，求函数的单调区间与极值；
（Ⅱ）若函数在上是增函数，求实数的取值范围．

将函数y=f（x）的图象沿x轴向左平移π个单位后，再将所得图象上各点的横坐标缩小为原来的一半，得到函数y=sinx的图象，那么y=f（x）的表达式为（ ）

A．y=sin2x

B．y=﹣sin2x

C．

D．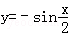

对于定义域为R的函数g（x），若存在正常数T，使得cosg（x）是以T为周期的函数，则称g（x）为余弦周期函数，则下列函数中余弦周期函数有多少个？（ ）
①h（x）=2016x 
②h（x）=|x|
③h（x）=x+sin．

A．0个

B．1个

C．2个

D．3个

要得到函数的图象，只需将的图象（    ）

A．向右平移个单位

B．向左平移个单位

C．向右平移个单位

D．向左平移个单位

函数y=sin（2x+）的图象的一条对称轴的方程是（ ）

A．x=﹣

B．x=﹣

C．x=

D．x=

下列函数中周期为π且图象关于直线x=对称的函数是（ ）

A．y=2sin（+）

B．y=2sin（2x﹣）

C．y=2sin（2x+）

D．y=2sin（﹣）

关于函数 $f\left(x\right)=4\sin (2x+\frac{\mathrm{\pi }}{3})(x\in R)$ ，有下列命题：
① $y=f\left(x\right)$ 的表达式可改写为 $y=4\cos (2x-\frac{\mathrm{\pi }}{6})$ ；
② $y=f\left(x\right)$ 是以 $2\pi$ 为最小正周期的周期函数；
③ $y=f\left(x\right)$ 的图象关于点 $\left(-\frac{\mathrm{\pi }}{6},0\right)$ 对称；
④ $y=f\left(x\right)$ 的图象关于直线 $x=-\frac{\mathrm{\pi }}{6}$ 对称．
其中正确的命题的序号是      ．

给出以下四个命题：
（1）当时，
（2）当时，
（3）已知与，则；
（4）在斜中，则
请在横线上填出所有正确命题的序号_________________．

将函数的图象上的各点的横坐标伸长到原来的2倍（纵坐标不变），再向左平移个单位，所得函数的图象的一条对称轴为（ ）

A．

B．

C．

D．x=π

下列各式的大小关系正确的是（ ）

A．sin11°＞sin168°

B．sin194°＜cos160°

C．cos（﹣）＞cos

D．tan（﹣）＜tan（﹣）

函数的部分图象如图所示，则函数解析式为________________．

函数 $f\left(x\right)=\sin x$ , $(\frac{\mathrm{\pi }}{6}\le x\le \frac{2\mathrm{\pi }}{3})$ 的值域为     ．

已知函数f（x）=2sinωx（ω＞0）在区间上的最小值是﹣2，则ω的最小值等于（ ）

A．

B．

C．2

D．3

设函数图象的一个对称轴方程是（    ）

A．

B．

C．

D．