高中数学多面角及多面角的性质试题

（本小题满分13分）某同学用“五点法”画函数（）在某一个周期内的图像时，列表并填入的部分数据如下表：

 
（1）请求出上表中的的值，并写出函数的解析式；
（2）将的图像向右平移个单位得到函数的图像，若函数在区间（）上的图像的最高点和最低点分别为，求向量与夹角的大小．

将函数的图象向左平移个单位得到函数的
图象，则函数是（ ）

A．周期为的奇函数	B．周期为的偶函数
C．周期为的奇函数	D．周期为的偶函数

已知向量，设函数。
（1）求函数 的最小正周期及时的最大值；
（2）把函数的图象向左平移个单位，所得到的图象对应的函数为奇函数，求的最小值。

下列对于函数 的判断正确的是 （   ）

A．函数的周期为

B．对于函数都不可能为偶函数

C．,使

D．函数在区间内单调递增

【改编题】已知函数的图象在轴右侧的第一个最高点和第一个最低点的坐标分别为和．
（1）求函数的解析式；
（2）求函数在区间上的最大值与最小值．

已知
（1）求函数的最小正周期及单调递增区间．
（2）当时，方程有实数解，求实数的取值范围．

已知函数（），相邻两对称轴之间的距离为．
（1）求函数的解析式；
（2）把函数的图象向右平移个单位，再纵坐标不变横坐标缩短到原来的后得到函数的图象，当 时，求函数的单调递增区间．

已知函数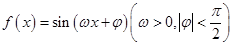的部分图象如图所示．

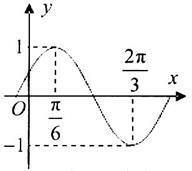
（1）求函数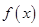的解析式，并写出 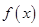的单调递减区间；
（2）已知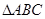的内角分别是A，B，C，角A为锐角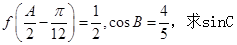，的值．

设函数f(x)＝＋2cos²x.
(1)求f(x)的最大值，并写出使f(x)取最大值时x的集合；
(2)已知△ABC中，角A，B，C的对边分别为a，b，c，若f(B＋C)＝，b＋c＝2，求a的最小值．

已知函数f(x)＝2sin xcos x＋2cos²x－，x∈R.
(1)求函数f(x)的最小正周期；
(2)在锐角△ABC中，若f(A)＝1，·＝，求△ABC的面积．

某同学用“五点法”画函数在某一个周期的图象时，列表并填入的部分数据如下表：

（1）求，，的值及函数的表达式；
（2）将函数的图象向左平移个单位，可得到函数的图象，求函数在区间的最小值．

下列命题正确的是（   ）
①函数的一个对称中心是；
②从装有2个红球和2个白球的袋内任取2个球，则事件“至少有1个红球”和事件“全是白球”是互斥而不对立的两个事件；
③ 将的图象向右平移个单位长度，即得到函数的图象；
④若函数的图象都在轴上方，则实数的取值范围是．

A．①③

B．①④

C．②④

D．③④

设满足约束条件，若目标函数的最大值为，则的图象向右平移后的表达式为___________．

设函数，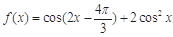
（Ⅰ）求的最大值，并写出使取最大值时x的集合；
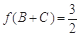（Ⅱ）已知中，角A、B、C的对边分别为a、b、c，若，，求的面积的最大值．

已知函数，且给定条件p：“”，
（1）求f（x）的最大值及最小值
（2）若又给条件q：“|f（x）﹣m|＜2“且p是q的充分条件，求实数m的取值范围．