(本小题满分13分)某同学用“五点法”画函数 (
(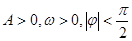 )在某一个周期内的图像时,列表并填入的部分数据如下表:
)在某一个周期内的图像时,列表并填入的部分数据如下表:
 |
 |
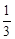 |
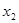 |
 |
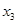 |
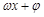 |
 |
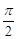 |
 |
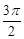 |
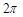 |
 |
 |
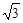 |
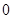 |
 |
 |
(1)请求出上表中的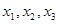 的值,并写出函数
的值,并写出函数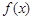 的解析式;
的解析式;
(2)将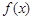 的图像向右平移
的图像向右平移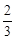 个单位得到函数
个单位得到函数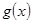 的图像,若函数
的图像,若函数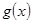 在区间
在区间 (
(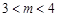 )上的图像的最高点和最低点分别为
)上的图像的最高点和最低点分别为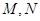 ,求向量
,求向量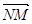 与
与 夹角
夹角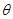 的大小.
的大小.
相关知识点
推荐套卷
 平面ABC.
平面ABC.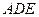 ;
;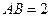 ,
, ,
, ,试求该简单组合体的体积V.
,试求该简单组合体的体积V.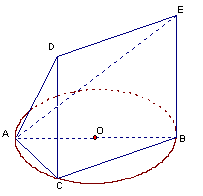
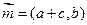 ,
,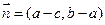 ,且
,且 ,其中
,其中 是△ABC的内角,
是△ABC的内角, 分别是角
分别是角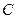 的大小;
的大小; 的取值范围.
的取值范围. 的前
的前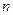 项和为
项和为
 满足
满足 ,
, 为数列
为数列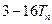 与
与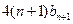 的大小,并证明你的结论.
的大小,并证明你的结论. 均在椭圆
均在椭圆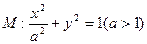 上,直线
上,直线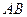 、
、 分别过椭圆的左右焦点
分别过椭圆的左右焦点 、
、 ,当
,当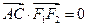 时,有
时,有 .
.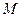 的方程;
的方程;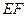 为圆
为圆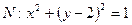 的任一条直径,求
的任一条直径,求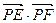 的最大值.
的最大值.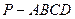 中,
中,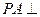 平面
平面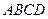 ,底面
,底面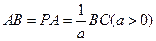 .
. 时,求证:
时,求证: ;
; 边上有且只有一个点
边上有且只有一个点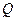 ,使得
,使得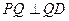 ,求此时二面角
,求此时二面角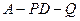 的余弦值.
的余弦值.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号