高中数学多面角及多面角的性质解答题

（本小题满分13分）
已知函数.
(1)求的单调递增区间；
(2)函数的图象经过怎样的平移可使其对应的函数成为偶函数? 请写出一种正确的平移方法，并说明理由.

已知向量， 
（1）  求在上的单调增区间；
（2）  若，求 的值

（本小题满分12分）
已知函数
（Ⅰ）求的最小正周期和单调递增区间；
（Ⅱ）求在区间上的最大值和最小值．

本小题满分12分）
已知函数
（1）求函数的最小正周期及函数取最小值时自变量的集合
（2）确定函数的单调递增区间
（3）若函数y=sin2x的图象向右平移m个单位(|m|<)，向上平移n个单位后得到函数y=f(x)的图象，求实数m、n的值

设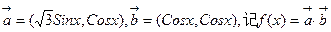
（1）写出函数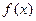的最小正周期；
（2）试用“五点法”画出函数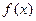在一个周期内的简图；
（3）若时，函数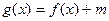的最小值为2，试求出函数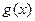的最大值。

已知函数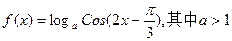
求：（1）函数的定义域和单调区间；
（2）判断函数的奇偶性；
（3）判断函数的周期性，如果是周期函数，求出它的最小正周期。

已知f(x)=2cos²x+sin2x+a (a∈R , a为常数)
(Ⅰ) 若x∈R , 求f(x)的单调增区间; 
(Ⅱ) 若x∈[0, ]时, f(x)的最大值为4, 并求此时f(x)的最小值。

（本小题分14分）已知函数
（Ⅰ）求的最小正周期T；
（Ⅱ）求的最大值和最小值；
（Ⅲ）求当取最大值时值的集合。

已知函数，
（1）  求函数的定义域及值域；
（2）  判断该函数的奇偶性，并证明你的结论.

（本小题满分12分）
已知函数=sin(2x+)+sin(2x-)+cos2x+1(xÎR)．
(1)化简并求的最小正周期；
(2)求函数的最大值及此时自变量x的取值集合；
(3)求使≥2的x的取值范围．

（本小题满分14分）
已知函数+1，求：
（1）求函数的单调减区间；
（2）求函数的最大值，以及函数取得最大值时自变量的集合

(本小题满分12分)
已知函数
(1)  求函数的最小正周期；
(2)  当时，求函数f (x) 的最大值与最小值及相应的值。

（本小题满分12分）
设函数，其中向量，，，且的图象经过点．（1）求实数的值；
（2）求函数的最小值及此时值的集合．

已知函数，求
（1）求的最小正周期及对称中心；
（2）当时，求的最大值和最小值.

(本题满分10分)已知函数

（1）求函数的最小正周期T；
（2）在给定坐标系中，用“五点法”作出函数在一个周期上的图像.
（3）把的图像向左平移个单位，得函数的图像，请判断函数的奇偶性.