已知f(x)=2cos2x+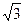 sin2x+a (a∈R , a为常数)
sin2x+a (a∈R , a为常数)
(Ⅰ) 若x∈R , 求f(x)的单调增区间;
(Ⅱ) 若x∈[0, 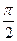 ]时, f(x)的最大值为4, 并求此时f(x)的最小值。
]时, f(x)的最大值为4, 并求此时f(x)的最小值。
相关知识点
推荐套卷
已知f(x)=2cos2x+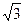 sin2x+a (a∈R , a为常数)
sin2x+a (a∈R , a为常数)
(Ⅰ) 若x∈R , 求f(x)的单调增区间;
(Ⅱ) 若x∈[0, 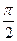 ]时, f(x)的最大值为4, 并求此时f(x)的最小值。
]时, f(x)的最大值为4, 并求此时f(x)的最小值。