已知函数
在x=
时取得最大值4..
(1)求
的最小正周期;
(2)求
的解析式;
(3)若
.求
的值.
已知函数f(x)=sinx+cosx.
(1)若f(x)=2f(﹣x),求 的值;
的值;
(2)求函数F(x)=f(x)•f(﹣x)+f2(x)的最大值和单调递增区间.
已知函数f(x)=sinxcosx﹣cos2x.
(1)求f(x)的最小正周期;
(2)求f(x)在区间 上的最小值,并求取得最小值时x的值.
上的最小值,并求取得最小值时x的值.
已知向量m=(sin ωx+ cosωx,1),n=(2cos ωx,-
cosωx,1),n=(2cos ωx,- )(ω>0),函数f(x)=m·n的两条相邻对称轴间的距离为
)(ω>0),函数f(x)=m·n的两条相邻对称轴间的距离为 .
.
(1)求函数f(x)的单调递增区间;
(2)当x∈[- ,
, ] 时,求f(x)的值域.
] 时,求f(x)的值域.
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|< )在x∈(0,7π)内取到一个最大值和一个最小值,且当x=π时,y有最大值3,当x=6π时,y有最小值-3.
)在x∈(0,7π)内取到一个最大值和一个最小值,且当x=π时,y有最大值3,当x=6π时,y有最小值-3.
(1)求此函数解析式;
(2)写出该函数的单调递增区间.
已知函数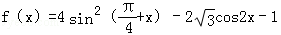 ,且给定条件p:“
,且给定条件p:“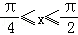 ”,
”,
(1)求f(x)的最大值及最小值
(2)若又给条件q:“|f(x)﹣m|<2“且p是q的充分条件,求实数m的取值范围.