已知向量m＝（sin ωx＋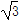
cosωx，1），n＝（2cos ωx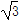，－）（ω>0），函数f（x）＝m·n的两条相邻对称轴间的距离为
．
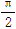（1）求函数f（x）的单调递增区间；
（2）当x∈[－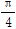
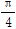，] 时，求f（x）的值域．
满足
，求证：
．
.
.
的解集;
对
恒成立,求实数a的取值范围.
.
；
的解集为
，求实数
的取值范围.
均为正实数，并且
，求证：
相关知识点
推荐套卷
已知向量m＝（sin ωx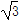＋cosωx，1），n＝（2cos ωx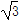，－）（ω>0），函数f（x）＝m·n的两条相邻对称轴间的距离为．
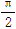（1）求函数f（x）的单调递增区间；
（2）当x∈[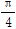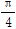－，] 时，求f（x）的值域．
粤公网安备 44130202000953号