为了调查某厂2000名工人生产某种产品的能力,随机抽查了 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为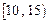 ,
,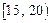 ,
,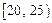 ,
, ,
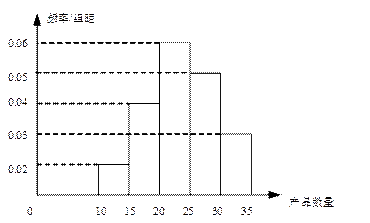
, ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在 之间的工人有6位.
之间的工人有6位.
⑴求 ;
;
⑵工厂规定从各组中任选1人进行再培训,则选取5人不在同一组的概率是多少?
相关知识点
推荐套卷
为了调查某厂2000名工人生产某种产品的能力,随机抽查了 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为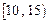 ,
,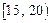 ,
,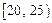 ,
, ,
, ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在 之间的工人有6位.
之间的工人有6位.
⑴求 ;
;
⑵工厂规定从各组中任选1人进行再培训,则选取5人不在同一组的概率是多少?