(本题满分10分)已知函数
（1）求函数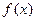
的最小正周期T；
（2）在给定坐标系中，用“五点法”作出函数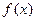在一个周期上的图像.
（3
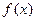）把的图像向左平移
个单位，得函数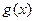
的图像，请判断函数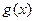的奇偶
性.
相关试题
，使得函数
在闭区间
上的最大值是
？若存在，求出对应的
，x∈R,(其中
)的图象与y轴交于点（0，1）. 
的值；
与
夹角的余弦值.
，向量
，函数
且当
时，求函数
的单调递减区间；
时，写出由函数
的图象变换到函数
的图象的变换过程.
.若关于
的方程
在
上有解，求实数
的取值范围.
已知定义在区间
上的函数
的图象关于直线
对称，当
时，函数
，
的解.相关知识点
推荐套卷
(本题满分10分)已知函数
（1）求函数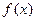的最小正周期T；
（2）在给定坐标系中，用“五点法”作出函数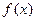在一个周期上的图像.
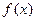（3）把的图像向左平移个单位，得函数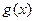的图像，请判断函数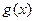的奇偶性.
粤公网安备 44130202000953号