高中数学多面角及多面角的性质解答题

（本小题满分12分）
已知函数．
（1）求函数的最小正周期和值域；
（2）若为第二象限角，且，求的值．

（本小题满分14分）
在中，角所对的边分别为，向量
，且.
（Ⅰ）求的值；   
（Ⅱ）若的面积为，求．

设函数，(w为常数，且m >0),已知函数f(x)的最大值为2.
(I)求函数的单调递减区间；
(II)已知a,b,c是的三边，且.若，，求B的值.

已知向量，函数（Ⅰ）求函数的最小正周期；（Ⅱ）将函数的图像向左平移上个单位后，再将所得图像上所有点的横坐标伸长为原来的3倍，得到函数的图像，求函数的解析式及其对称中心坐标.

（本小题满分14分）
已知函数．]
（1）求函数的最小值和最小正周期；
（2）设的内角、、的对边分别为，，，且，，若，求，的值．

已知函数。若，，求的最大值；在中，若，，求的值。

(本小题满分13分)
已知向量，，函数．
（1）求函数的最小正周期；
（2）若时，求的值域.

已知向量，，函数，．
（Ⅰ）求函数的最小正周期；
（Ⅱ）在中，分别是角的对边，R为外接圆的半径，且，，，且，求的值．

设函数
（1）求函数的最小正周期和单调递增区间；
（2）当时，的最大值为2，求的值，并求出的对称
轴方程．

（若，，定义：
已知，，，
（1）  若，且，求；
（2）  若函数的图象向左（或右）平移个单位，再向上（或
（3）  下）平移个单位后得到函数的图象，求实数的值．

已知
（1）求的最大值，及当取最大值时x的取值集合。
（2）在三角形ABC中，a，b，c分别是角A，B，C所对的边，对定义域内任意x，有的最大值．

（本小题满分12分）
已知向量，，且
（1）求的取值范围；
（2）求函数的最小值，并求此时x的值

(本题满分14分) 已知角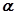的顶点在原点，始边与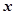轴的正半轴重合，终边经过点.
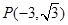（Ⅰ）求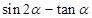的值；
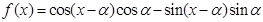（Ⅱ）若函数，求函数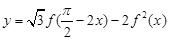
在区间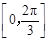上的取值范围．

已知三角函数.
(1)求出该函数的单调区间；
(2)用“五点作图法”做出该函数在一个周期内的图像.

已知函数；的图像经过点，且时，有最大值。
（1）求的解析式；
（2）能否通过平移变换，使得的图像关于原点对称，如果能，请写出这个变换，如果不能，试说明理由