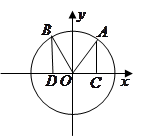
(本小题满分13分)如图,在平面直角坐标系 中,点
中,点 在单位圆
在单位圆 上,
上,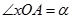 ,且
,且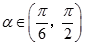 .
.
(1)若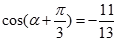 ,求
,求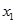 的值;
的值;
(2)若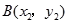 也是单位圆
也是单位圆 上的点,且
上的点,且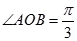 .过点
.过点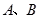 分别做
分别做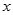 轴的垂线,垂足为
轴的垂线,垂足为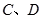 ,记
,记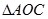 的面积为
的面积为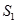 ,
, 的面积为
的面积为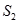 .设
.设 ,求函数
,求函数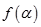 的最大值.
的最大值.
设函数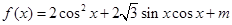
(1)求函数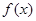 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)若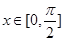 ,是否存在实数
,是否存在实数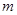 ,使函数
,使函数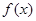 的值域恰为
的值域恰为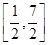 ?若存在,请求出
?若存在,请求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
已知函数 .
(1)求
的最小正周期和最大值;
(2)讨论
在
上的单调性.
(本小题满分12分)已知函数
 在一个周期内的图象如图所示,其中
在一个周期内的图象如图所示,其中
 ,
,
 .
.
(1)求函数 的解析式;
的解析式;
(2)在 中,角
中,角 的对边分别是
的对边分别是 ,且
,且 ,求
,求 的面积.
的面积.
(本小题满分14分)已知函数 ,
, , 其中,
, 其中, 是自然对数的底数.函数
是自然对数的底数.函数 ,
, .
.
(Ⅰ)求 的最小值;
的最小值;
(Ⅱ)将 的全部零点按照从小到大的顺序排成数列
的全部零点按照从小到大的顺序排成数列 ,求证:
,求证:
(1) ,其中
,其中 ;
;
(2) .
.
(本小题满分13分)已知函数


 的最小正周期为
的最小正周期为 .
.
(1)求 的值;
的值;
(2)将函数 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的 ,纵坐标不变,得到函
,纵坐标不变,得到函
数 的图象,求函数
的图象,求函数 在区间
在区间 上的最小值.
上的最小值.
(本小题满分12分)
已知函数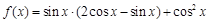 .
.
(Ⅰ)讨论函数 在
在 上的单调性;
上的单调性;
(Ⅱ)设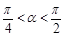 ,且
,且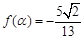 ,求
,求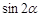 的值.
的值.