(本小题满分l2分)(注意:在试题卷上作答无效)
已知: 为常数)
为常数)
(I)若 ,求
,求 的最小正周期;
的最小正周期;
(Ⅱ)若 在x∈
在x∈ 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求 的值;
的值;
(Ⅲ)在(2)条件下 先按
先按 平移后再经过伸缩变换后得到
平移后再经过伸缩变换后得到 求
求 .
.
已知 ,
,
(Ⅰ) 求 的最大值及此时
的最大值及此时 的值;
的值;
(Ⅱ) 求 在定义域上的单调递增区间。
在定义域上的单调递增区间。
已知函数
(Ⅰ)若 ,求
,求 的最大值及取得最大
的最大值及取得最大 值时相应的x的值
值时相应的x的值
(Ⅱ)在△ABC中,a、b、c分别为角A、B、C的对边,若 ,b=l,
,b=l, ,求a的值
,求a的值
(本小题满分12分)巳知函数 .
.
(I)求函数 的最小正周期及在区间
的最小正周期及在区间 上的最大值和最小
上的最大值和最小 值;
值;
(II)若 ,求
,求 的值.
的值.
(1)利用“五点法”画出函数 在长度为一个周期的闭
在长度为一个周期的闭
区间的简图
列表: 作图:
(2)并说明该函数图象可由y=sinx(x R)的图象经过怎样的变换得到。
R)的图象经过怎样的变换得到。
已知函数f(x)=A (A>0,
(A>0,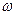 >0,0<
>0,0<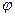 <
<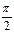 ,且y=f(x)的最大值为2,其
,且y=f(x)的最大值为2,其
图象相邻两对称轴间的距离为2,并过点(1,2).
(1)求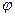 ;
;
(2)计算f (1) + f (2) +… + f ( 2 008 ).
是否存在实数a,使得函数y=sin2x+a·cos x+a-在闭区间上的最大值是1?若存在,求出对应的a值;若不存在,试说明理由