若函数
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)当
 时,求函数
时,求函数 的最大值与最小值.
的最大值与最小值.
如图,有两条相交成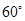 角的直路
角的直路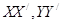 ,交点为
,交点为 ,甲、乙分别在
,甲、乙分别在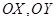 上,起初甲离
上,起初甲离 点
点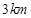 ,乙离
,乙离 点
点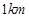 ,后来甲沿
,后来甲沿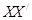 的方向,乙沿
的方向,乙沿 的方向,同时以
的方向,同时以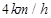 的速度步行。
的速度步行。
(1)起初两人的距离是多少?
(2)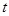 小时后两人的距离是多少?
小时后两人的距离是多少?
(3)什么时候两人的距离最短,并求出最短距离。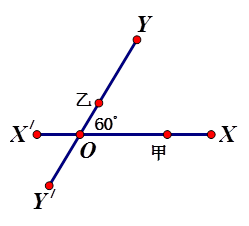
已知函数
(1) 求函数 的最小正周期; (2) 求函数
的最小正周期; (2) 求函数 在区间
在区间 上的值域;
上的值域;
(3)借助”五点作图法”画出函数 在
在 上的简图,并且依图写出函数
上的简图,并且依图写出函数 在
在 上的递增区间.
上的递增区间.
把函数 的图像上每一点的横坐标伸长到原来的2倍,纵坐标不变,然后再向左平移
的图像上每一点的横坐标伸长到原来的2倍,纵坐标不变,然后再向左平移 个单位后得到一个最小正周期为2
个单位后得到一个最小正周期为2 的奇函数
的奇函数 .
.
(1) 求 的值;
的值;
(2) 的单调区间和最值.
的单调区间和最值.
已知 为坐标原点,
为坐标原点, ,
, (
( ,
, 是常数),若
是常数),若 .
.
(1)求 关于
关于 的函数关系式
的函数关系式 ;
;
(2)若 的最大值为
的最大值为 ,求
,求 的值;
的值;
(3)利用(2)的结论,用“五点法”作出函数 在长度为一个周期的闭区间上的简图,并指出函数
在长度为一个周期的闭区间上的简图,并指出函数 的单调区间
的单调区间
若函数f(x)=sin2ax- sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为
sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为 .
.
(1)求m和a的值;
(2)若点A(x0,y0)是y=f(x)图象的对称中心,且x0∈ ,求点A的坐标.
,求点A的坐标.
 、
、 、
、 为
为 的三内角,且其对边分别为
的三内角,且其对边分别为 、b、c,若
、b、c,若 ,
, ,且
,且 .
.
(Ⅰ) 求角 ;
;
(Ⅱ) (只文科做)若 ,三角形面积
,三角形面积 ,求
,求 的值
的值
(只理科做)若 ,求2b+c的取值范围.
,求2b+c的取值范围.
已知函数 .
.
(1)求函数 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)求函数 在区间
在区间 上的值域.
上的值域.