已知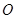 为坐标原点,
为坐标原点,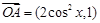 ,
,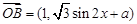 (
(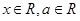 ,
,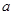 是常数),若
是常数),若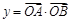 .
.
(1)求 关于
关于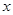 的函数关系式
的函数关系式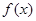 ;
;
(2)若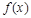 的最大值为
的最大值为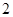 ,求
,求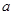 的值;
的值;
(3)利用(2)的结论,用“五点法”作出函数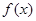 在长度为一个周期的闭区间上的简图,并指出函数
在长度为一个周期的闭区间上的简图,并指出函数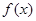 的单调区间
的单调区间
相关知识点
推荐套卷
已知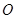 为坐标原点,
为坐标原点,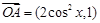 ,
,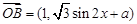 (
(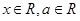 ,
,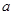 是常数),若
是常数),若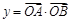 .
.
(1)求 关于
关于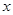 的函数关系式
的函数关系式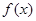 ;
;
(2)若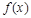 的最大值为
的最大值为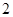 ,求
,求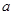 的值;
的值;
(3)利用(2)的结论,用“五点法”作出函数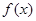 在长度为一个周期的闭区间上的简图,并指出函数
在长度为一个周期的闭区间上的简图,并指出函数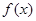 的单调区间
的单调区间