设函数 。
。
(1)求函数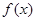 的最小正周期;
的最小正周期;
(2)设函数 对任意
对任意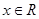 ,有
,有 ,且当
,且当 时,
时, 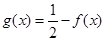 ,求函数
,求函数 在
在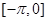 上的解析式.
上的解析式.
(本小题满分12分)若向量

 =
= ,在函数
,在函数
 +
+ 的图象中,对称中心到对称轴的最小距离为
的图象中,对称中心到对称轴的最小距离为 ,且当
,且当 时,
时,  的最大值为
的最大值为 .
.
(1)求函数 的解析式;
的解析式;
(2)求函数 的单调递增区间.
的单调递增区间.
(本题满分14分)在 中,
中, 分别是角
分别是角 ,
, ,
, 的对边,且
的对边,且 .
.
(I)若函数 求
求 的单调增区间;
的单调增区间;
(II)若 ,求
,求 面积的最大值.
面积的最大值.
(本小题满分12分)已知函数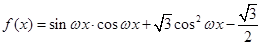 (
(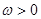 ),直线
),直线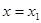 ,
,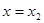 是
是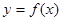 图象的任意两条对称轴,且
图象的任意两条对称轴,且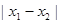 的最小值为
的最小值为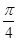 .
.
(I)求 的表达式;
的表达式;
(Ⅱ)将函数 的图象向右平移
的图象向右平移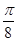 个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数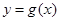 的图象,若关于
的图象,若关于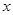 的方程
的方程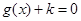 ,在区间
,在区间 上有且只有一个实数解,求实数
上有且只有一个实数解,求实数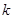 的取值范围.
的取值范围.
已知:在 中,
中,  、
、 、
、 分别为角
分别为角 、
、 、
、 所对的边,且角
所对的边,且角 为锐角,
为锐角,
(Ⅰ)求 的值;
的值;
(Ⅱ)当 ,
, 时,求
时,求 及
及 的长.
的长.
(本小题满分12分) 已知函数
已知函数 ,
, .
.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)求函数 在区间
在区间 上的最小值和最大值,并求出取得最值时
上的最小值和最大值,并求出取得最值时 的值.
的值.
(本题满分12 分)
(1)计算 ,
,
(2)已知 ,求sin
,求sin 的值。
的值。