[上海]2013届上海市奉贤区高考一模理科数学试卷
在平面直角坐标系 中,对于任意两点
中,对于任意两点 与
与 的“非常距离”
的“非常距离”
给出如下定义:若 ,则点
,则点 与点
与点 的“非常距离”为
的“非常距离”为 ,
,
若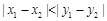 ,则点
,则点 与点
与点 的“非常距离”为
的“非常距离”为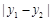 .
.
已知 是直线
是直线 上的一个动点,点
上的一个动点,点 的坐标是(0,1),则点
的坐标是(0,1),则点 与点
与点 的“非常距离”的最小值是_________.
的“非常距离”的最小值是_________.
来源:2013届上海市奉贤区高考一模理科数学试题
设 ,则“
,则“ ”是“
”是“ ”的 ( )
”的 ( )
| A.充分而不必要条件; | B.必要而不充分条件; |
| C.充分必要条件; | D.既不充分也不必要条件; |
来源:2013届上海市奉贤区高考一模理科数学试题
已知 是等差数列
是等差数列 的前n项和,且
的前n项和,且 ,有下列四个命
,有下列四个命
题,假命题的是( )
A.公差 ; ; |
B.在所有 中, 中, 最大; 最大; |
C.满足 的 的 的个数有11个; 的个数有11个; |
D. ; ; |
来源:2013届上海市奉贤区高考一模理科数学试题
定义域是一切实数的函数 ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数 (
( )
)
使得 对任意实数
对任意实数 都成立,则称
都成立,则称 是一个“
是一个“ —伴随函数”. 有
—伴随函数”. 有
下列关于“ —伴随函数”的结论:
—伴随函数”的结论:
① 是常数函数中唯一一个“
是常数函数中唯一一个“ —伴随函数”;
—伴随函数”;
②“ —伴随函数”至少有一个零点;
—伴随函数”至少有一个零点;
③ 是一个“
是一个“ —伴随函数”;
—伴随函数”;
其中正确结论的个数是 ( )
| A.1个; | B.2个; | C.3个; | D.0个; |
来源:2013届上海市奉贤区高考一模理科数学试题
某海域有 、
、 两个岛屿,
两个岛屿, 岛在
岛在 岛正东4海里处。经多年观察研究发现,某种鱼群洄游的路线是曲线
岛正东4海里处。经多年观察研究发现,某种鱼群洄游的路线是曲线 ,曾有渔船在距
,曾有渔船在距 岛、
岛、 岛距离和为8海里处发现过鱼群。以
岛距离和为8海里处发现过鱼群。以 、
、 所在直线为
所在直线为 轴,
轴, 的垂直平分线为
的垂直平分线为 轴建立平面直角坐标系。
轴建立平面直角坐标系。
(1)求曲线 的标准方程;
的标准方程;
(2)某日,研究人员在 、
、 两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),
两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同), 、
、 两岛收到鱼群在
两岛收到鱼群在 处反射信号的时间比为
处反射信号的时间比为 ,问你能否确定
,问你能否确定 处的位置(即点
处的位置(即点 的坐标)?
的坐标)?
来源:2013届上海市奉贤区高考一模理科数学试题
定义数列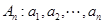 ,(例如
,(例如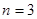 时,
时, )满足
)满足 ,且当
,且当 (
( )时,
)时, .令
.令 .
.
(1)写出数列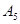 的所有可能的情况;
的所有可能的情况;
(2)设 ,求
,求 (用
(用
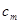 的代数式来表示);
的代数式来表示);
(3)求 的最大值.
的最大值.
来源:2013届上海市奉贤区高考一模理科数学试题
 的方程
的方程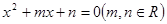 的一个根是
的一个根是 ,则
,则 _________.
_________. 的最小正周期为 .
的最小正周期为 . ,
, ,则
,则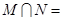 _________.
_________. :
: 的方向向量是
的方向向量是 ,直线
,直线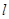 2 :
2 : 的法向量是
的法向量是 ,若
,若 _________.
_________. 且
且 若
若 恒成立,则实数m的取值范围是_________.
恒成立,则实数m的取值范围是_________. 的前n项和为Sn,首项是
的前n项和为Sn,首项是 ,若
,若 Sn=
Sn=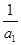 ,
, ,则公比
,则公比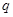 的取值范围是 .
的取值范围是 . 为奇函数,则
为奇函数,则 .
. 、
、 的二元线性方程组
的二元线性方程组 的增广矩阵经过变换,最后得到的矩阵为
的增广矩阵经过变换,最后得到的矩阵为 ,则二阶行列式
,则二阶行列式 = .
= . 那么
那么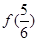 的值为 .
的值为 . 的最大值为_________.
的最大值为_________. 的反函数是
的反函数是 ,且
,且 过点
过点 ,则
,则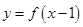 经过点 .
经过点 . 是
是 上的偶函数,
上的偶函数, 是
是 ,
, ,则
,则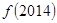 的值为_________.
的值为_________. ,
, 是公差为
是公差为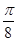 的等差数列,
的等差数列, ,则
,则 .
. 的图像如左图所示,则函数
的图像如左图所示,则函数 的图像可能是( )
的图像可能是( )
 ,
, ,
,
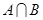 ,
, 的取值范围.
的取值范围. 。
。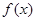 的最小正周期;
的最小正周期; 对任意
对任意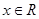 ,有
,有 ,且当
,且当 时,
时, 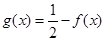 ,求函数
,求函数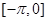 上的解析式.
上的解析式.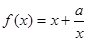 定义域为
定义域为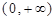 ,且
,且 .
. 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点 和
和 轴的垂线,垂足分别为
轴的垂线,垂足分别为 .
.
 的单调递减区间(不必证明);
的单调递减区间(不必证明);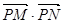 是否为定值?若是,则求出该定值,若不是,则说明理由;
是否为定值?若是,则求出该定值,若不是,则说明理由; 为坐标原点,求四边形
为坐标原点,求四边形 面积的最小值.
面积的最小值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号