[浙江]2012届浙江省三校高三联考理科数学
从集合 中随机选取一个数记为
中随机选取一个数记为 ,从集合
,从集合 中随机选取一个数记为
中随机选取一个数记为 ,则直线
,则直线 不经过第三象限的概率为 ( ▲ )
不经过第三象限的概率为 ( ▲ )
A. |
B. |
C. |
D. |
在圆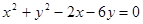 内,过点E(0,1)的最长弦和最短弦分别是AC和BD,则四边形ABCD的面积为 ( ▲ )
内,过点E(0,1)的最长弦和最短弦分别是AC和BD,则四边形ABCD的面积为 ( ▲ )
A.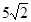 |
B.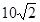 |
C.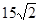 |
D.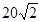 |
在长方体ABCD—A1B1C1D1中,过长方体的顶点A与长方体12条棱所成的角都相等的平面有 ( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知函数 则“
则“ ”是“
”是“ 在
在 上单调递减”的( ▲ )
上单调递减”的( ▲ )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
设双曲线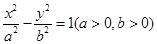 的左、右焦点分别是
的左、右焦点分别是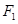 、
、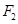 ,过点
,过点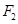 的直线交双曲线右支于不同的两点
的直线交双曲线右支于不同的两点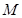 、
、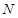 .若△
.若△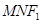 为正三角形,则该双曲线的离心率为(▲)
为正三角形,则该双曲线的离心率为(▲)
A.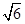 |
B.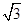 |
C.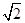 |
D.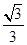 |
设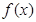 是定义在
是定义在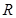 上的奇函数,且当
上的奇函数,且当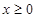 时,
时,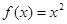 . 若对任意的
. 若对任意的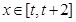 ,不等式
,不等式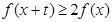 恒成立,则实数
恒成立,则实数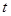 的取值范围是 ( ▲ )
的取值范围是 ( ▲ )
A.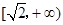 |
B. |
C.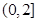 |
D.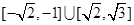 |
将“你能HOLD住吗”8个汉字及英文字母填入5×4的方格内,其中“你”字填入左上角,“吗”字填入右下角,将其余6个汉字及英文字母依次填入方格,要求只能横读或竖读成一句原话,如图所示为一种填法,则共有___▲ 种不同的填法。(用数字作答)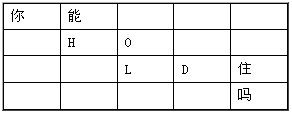
设函数 的定义域为
的定义域为 ,若存在非零实数
,若存在非零实数 使得对于任意
使得对于任意 ,有
,有 ,则称
,则称 为
为 上的“
上的“ 调函数”.如果定义域是
调函数”.如果定义域是 的函数
的函数 为
为 上的“
上的“ 调函数”,那么实数
调函数”,那么实数 的取值范围是___▲ .
的取值范围是___▲ .
(本题满分14分) 已知角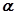 的顶点在原点,始边与
的顶点在原点,始边与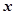 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点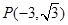 .
.
(Ⅰ)求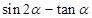 的值;
的值;
(Ⅱ)若函数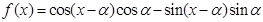 ,求函数
,求函数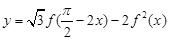 在区间
在区间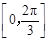 上的取值范围.
上的取值范围.
(本题满分14分) 已知数列 的首项
的首项
 ,
, ,
,
(1)若 ,求证
,求证 是等比数列并求出
是等比数列并求出 的通项公式;
的通项公式;
(2)若 对一切
对一切 都成立,求
都成立,求 的取值范围。
的取值范围。
(本小题满分14分)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=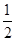 AD=1,CD=
AD=1,CD=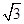 .
.
(1)求证:平面PQB⊥平面PAD;
(2)若二面角M-BQ-C为30°,设PM=tMC,
试确定t的值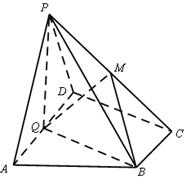
(本题满分15分) 已知抛物线 的顶点是椭圆
的顶点是椭圆 的中心,焦点与该椭圆的右焦点重合.
的中心,焦点与该椭圆的右焦点重合.
(1)求抛物线 的方程;
的方程;
(2)已知动直线 过点
过点 ,交抛物线
,交抛物线 于
于 、
、 两点.
两点. 若直线
若直线 的斜率为1,求
的斜率为1,求 的长;
的长; 是否存在垂直于
是否存在垂直于 轴的直线
轴的直线 被以
被以 为直径的圆
为直径的圆 所截得的弦长恒为定值?如果存在,求出
所截得的弦长恒为定值?如果存在,求出 的方程;如果不存在,说明理由.
的方程;如果不存在,说明理由.
(本小题满分15分)设 ,函数
,函数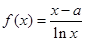 ,
, .
.
(1)当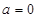 时,比较
时,比较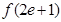 与
与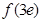 的大小;
的大小;
(2)若存在实数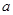 ,使函数
,使函数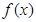 的图象总在函数
的图象总在函数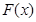 的图象的上方,求
的图象的上方,求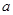 的取值集合.
的取值集合.
数学自选模块
题号:03
“数学史与不等式选讲”模块
已知函数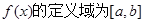 ,且
,且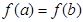 ,对于定义域内的任意实数
,对于定义域内的任意实数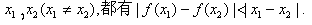 (1)设
(1)设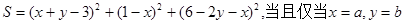 时,S取得最小值,求a,b的值;(2)在(1)的条件下,证明:对任意
时,S取得最小值,求a,b的值;(2)在(1)的条件下,证明:对任意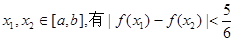 成立.
成立.
 得 ( ▲ )
得 ( ▲ )



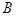 的值是( ▲ )
的值是( ▲ )
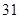
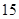
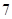
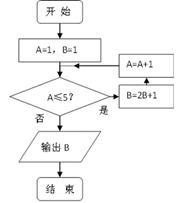
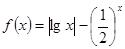 有两个零点
有两个零点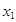 、
、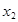 ,则有 ( ▲ )
,则有 ( ▲ )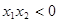
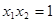
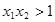
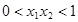
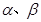 均为锐角,且
均为锐角,且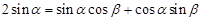 ,则
,则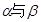 的大小关系为( ▲ )
的大小关系为( ▲ )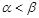
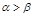

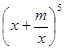 的展开式中
的展开式中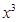 的系数为
的系数为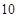 ,则实数
,则实数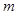 等于___▲ .
等于___▲ .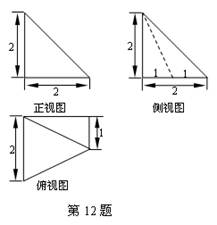
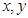 满足约束条件
满足约束条件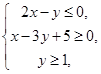 则
则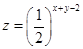 的最大值等于___▲ .
的最大值等于___▲ .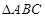 中,角
中,角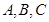 所对的边分别是
所对的边分别是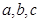 ,若
,若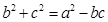 ,
,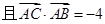 ,则
,则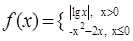 , 若关于x的函数
, 若关于x的函数 有8个不同的零点,则实数b的取值范围是___▲ .
有8个不同的零点,则实数b的取值范围是___▲ .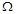 由圆弧ACB和圆弧BDA组成.已知
由圆弧ACB和圆弧BDA组成.已知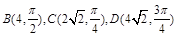

 粤公网安备 44130202000953号
粤公网安备 44130202000953号