 ,则称
,则称 为
为 与
与
在 上的一个“分界函数”.如
上的一个“分界函数”.如 ,则称
,则称 一个“分界函数”。
一个“分界函数”。
(1)求证: 是
是 和
和 在
在 上的一个“分界函数”;
上的一个“分界函数”;
(2)若 和
和 在
在 上一定存在一个“分界函数”,试确定实数
上一定存在一个“分界函数”,试确定实数 的取值范围.
的取值范围.
已知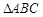 的三内角分别为
的三内角分别为 ,向量
,向量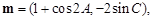
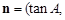
 ,记函数
,记函数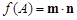 .
.
(1)若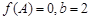 ,求
,求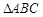 的面积;
的面积;
(2)若关于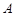 的方程
的方程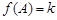 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.
第一小题3分,第二小题5分,第三小题6分.
(1)已知函数 是奇函数,
是奇函数, 为常数,求实数
为常数,求实数 的值;
的值;
(2)若 ,且
,且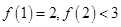 ,求
,求 的解析式;
的解析式;
(3)对于(2)中的 ,若
,若 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
定义:对于函数 ,若存在非零常数
,若存在非零常数 ,使函数
,使函数 对于定义域内的任意实数
对于定义域内的任意实数 ,都有
,都有 ,则称函数
,则称函数 是广义周期函数,其中称
是广义周期函数,其中称 为函数
为函数 的广义周期,
的广义周期, 称为周距.
称为周距.
(1)证明函数 是以2为广义周期的广义周期函数,并求出它的相应周距
是以2为广义周期的广义周期函数,并求出它的相应周距 的值;
的值;
(2)试求一个函数 ,使
,使 (
( 为常数,
为常数, )为广义周期函数,并求出它的一个广义周期
)为广义周期函数,并求出它的一个广义周期 和周距
和周距 ;
;
(3)设函数 是周期
是周期 的周期函数,当函数
的周期函数,当函数 在
在 上的值域为
上的值域为 时,求
时,求 在
在 上的最大值和最小值.
上的最大值和最小值.
设函数
.
(Ⅰ)若当
时
取得极值,求
的值,并讨论
的单调性;
(Ⅱ)若
存在极值,求
的取值范围,并证明所有极值之和大于
.
已知函数 ,满足
,满足 .
.
(1)求常数c的值;
(2)解关于 的不等式
的不等式 .
.
(本小题满分13分)对于定义域为D的函数 ,若同时满足下列条件:①
,若同时满足下列条件:① 在D内单调递增或单调递减;②存在区间[
在D内单调递增或单调递减;②存在区间[ ]
] ,使
,使 在[
在[ ]上的值域为[
]上的值域为[ ];那么把
];那么把 (
( )叫闭函数。
)叫闭函数。
(1)求闭函数 符合条件②的区间[
符合条件②的区间[ ];
];
(2)判断函数 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)判断函数 是否为闭函数?若是闭函数,求实数
是否为闭函数?若是闭函数,求实数 的取值范围。
的取值范围。
(本小题满分12 分)
分)
设函数f(x)的定义域为R,若|f(x)|≤|x|对任意的实数x均成立,则称函数f(x)为 函数。
函数。
(1)试判断函数 =
=
 =
= 中哪些是
中哪些是 函数,并说明理由;
函数,并说明理由;
(2)求证:若a>1,则函数f(x)=ln(x2+a)-lna是 函数。
函数。
(本小题满分14分)对于定义在区间D上的函数 ,若存在闭区间
,若存在闭区间 和常数
和常数 ,使得对任意
,使得对任意 ,都有
,都有 ,且对任意
,且对任意 ∈D,当
∈D,当 时,
时, 恒成立,则称函数
恒成立,则称函数 为区间D上的“平底型”函数.
为区间D上的“平底型”函数.
(Ⅰ)判断函数 和
和 是否为R上的“平底
是否为R上的“平底 型”函数? 并说明理由;
型”函数? 并说明理由;
(Ⅱ)设 是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式
是(Ⅰ)中的“平底型”函数,k为非零常数,若不等式 对一切
对一切 R恒成立,求实数
R恒成立,求实数 的取值范围;
的取值范围;
(Ⅲ)若函数 是区间
是区间 上的“平底型”函数,求
上的“平底型”函数,求 和
和 的值.
的值.
.
(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
已知二次函数
 对任意
对任意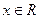 均有
均有 成立,且函数的图像过点
成立,且函数的图像过点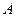
 .
.
(1)求函数 的解析式;
的解析式;
(2)若不等式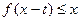 的解集为
的解集为 ,求实数
,求实数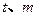 的值.
的值.
已知函数 (
( ).
).
(1)若 ,求函数
,求函数 的极值;
的极值;
(2)若 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.