高中数学函数迭代解答题

（本小题满分14分）已知函数有下列性质：“若
，使得”成立。
（1）利用这个性质证明唯一；
（2）设A、B、C是函数图象上三个不同的点，试判断△ABC的形状，并说明理由。

给定函数和常数，若恒成立，则称为函数的一个“好数对”；若恒成立，则称为函数的一个“类好数对”．已知函数的定义域为．
（Ⅰ）若是函数的一个“好数对”，且，求；
（Ⅱ）若是函数的一个“好数对”，且当时，，求证：
函数在区间上无零点；
（Ⅲ）若是函数的一个“类好数对”，，且函数单调递增，比较与的大小，并说明理由．

已知函数.
(1)求函数的单调区间；
(2)若，求函数的值域.

已知函数在上是减函数，在上是增函数，函数在上有三个零点，且1是其中一个零点．
（1）求的值；
（2）求的取值范围；
（3）试探究直线与函数的图像交点个数的情况，并说明理由．

已知函数.
（1）解关于的不等式；
（2）若在区间上恒成立，求实数的取值范围.

（本小题满分12分）设函数在上的导函数为，在上的导函数为，若在上，恒成立，则称函数在上为“凸函数”．已知．
（1）若为区间上的“凸函数”，试确定实数的值；
（2）若当实数满足时，函数在上总为“凸函数”，求的最大值．

已知是定义域为上的增函数，，且，指出单调区间，并证明你的结论．

已知是定义在的函数，满足．设，．当时，．分别求当、、时，的表达式、、．

东方旅社有100张普通客床，若每床每夜收租费10元时，客床可以全部租出；若每床每夜收费提高2元，便减少10张客床租出；若再提高2元，便再减少10张客床租出．依此情况变化下去．为了投资少而获租金最多，每床每夜应提高租金多少元？

已知函数（a为常数）在x=1处的切线的斜率为1．
(1)求实数a的值，并求函数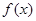的单调区间，
(2)若不等式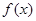≥k在区间上恒成立，其中e为自然对数的底数，求实数k的取值范围．

已知开口向上的二次函数f(x)，对任意，恒有
成立，设向量a=，b=(1,2)。
求不等式f(a·b)<f(5)的解集。

设函数
（I）求函数的单调区间；
（II）若不等式（）在上恒成立，求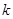的最大值.

已知：的最小值。

设是方程的两个实根，则的最小值是多少？

（本小题满分12分）定义在上的函数，如果满足：对任意，存在常数，都有成立，则称是上的有界函数，其中称为函数的上界.已知函数，
（1）当时，求函数在上的值域，并判断函数在上是否为有界函数，请说明理由；
（2）若函数在上是以4为上界的有界函数，求实数的取值范围.