高中数学函数迭代解答题

已知是定义在上的奇函数，且，若时，有成立.
（1）判断在上的单调性，并证明；
（2）解不等式：；
（3）若当时，对所有的恒成立，求实数的取值范围.

设，（1）分别求；（2）然后归纳猜想一般性结论，并给出证明.

（本小题满分13分）已知函数（）在区间上有最大值和最小值．设．
(1）求、的值；
(2）若不等式在上有解，求实数的取值范围.

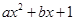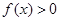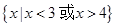已知函数，(1) 若的解集是，求实数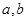的值；(2) 若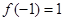且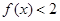恒成立，求实数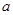的取值范围.

若定义在上的函数同时满足：①；②；③若，且，则成立.则称函数为“梦函数”.
（1）试验证在区间上是否为“梦函数”；
（2）若函数为“梦函数”，求的最值.

设，时，的最小值是-1，最大值是1，求、的值.

设 $a>0,b>0$，已知函数 $f\left(x\right)=\frac{ax+b}{x+1}$．
（Ⅰ）当 $a\ne b$时，讨论函数 $f\left(x\right)$的单调性；
（Ⅱ）当 $x>0$时，称 $f\left(x\right)$为 $a,b$关于 $x$的加权平均数．
（1）判断 $f\left(1\right),f\left(\sqrt{\frac{b}{a}}\right),f\left(\frac{b}{a}\right)$是否成等比数列，并证明 $f\left(\frac{b}{a}\right)\le f\left(\sqrt{\frac{b}{a}}\right)$；
（2） $a,b$的几何平均数记为 $G$．称 $\frac{2ab}{a+b}$为 $a,b$的调和平均数，记为 $H$．若 $H\le f\left(x\right)\le G$，求 $x$的取值范围．

设 x₁、x₂（）是函数 （）的两个极值点．
（I）若 ，，求函数  的解析式；
（II）若 ，求 b 的最大值；

(文)已知函数在区间上最大值为1，最小值为2．（1）求的解析式；（2）若函数在区间上为减函数，求实数m的取值范围．

对于函数f（x），若存在x₀∈R，使f（x₀）=x₀成立，则称x₀为f（x）的不动点．已知函数f（x）=ax²+（b+1）x+b﹣1（a≠0）．
（1）当a=1，b=﹣2时，求f（x）的不动点；
（2）若对于任意实数b，函数f（x）恒有两个相异的不动点，求a的取值范围．

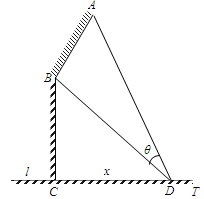
如图，某机场建在一个海湾的半岛上，飞机跑道AB的长为4.5km，且跑道所在的直线与海岸线l的夹角为60^o(海岸线可以看作是直线)，跑道上离海岸线距离最近的点B到海岸线的距离BC＝4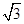km．D为海湾一侧海岸线CT上的一点，设CD＝x(km)，点D对跑道AB的视角为q．
（1）将tanq表示为x的函数；
（2）求点D的位置，使q取得最大值．

已知函数f(x)＝ax＋ (x≠0，常数a∈R)．
(1)讨论函数f(x)的奇偶性，并说明理由；
(2)若函数f(x)在x∈[3，＋∞)上为增函数，求a的取值范围．

（本小题满分10分） 已知（），是关于的次多项式；
（1）若恒成立，求和的值；并写出一个满足条件的的表达式，无需证明．
（2）求证：对于任意给定的正整数，都存在与无关的常数，，，…，，
使得．

已知函数y=
（Ⅰ）求函数y的最小正周期；
（Ⅱ）求函数y的最大值．

已知函数，常数．
（1）讨论函数的奇偶性，并说明理由；
（2）若函数在上为增函数，求的取值范围．