高中数学函数迭代解答题

已知函数的定义域，若在上为增函数，则称为“一阶比增函数”；若在上为增函数，则称为“二阶比增函数”。把所有由“一阶比增函数”组成的集合记为，把所有由“二阶比增函数”组成的集合记为．（1）已知函数，若且，求实数的取值范围；
（2）已知，且存在常数，使得对任意的，都有，求的最小值．

已知函数是幂函数且在上为减函数，函数在区间上的最大值为2，试求实数的值。

若在定义域内存在实数x₀，使得f（x₀+1）=f（x₀）+f（1）成立，则称函数f（x）是“可拆函数”．
（1）函数f（x）=是否是“可拆函数”？请说明理由；
（2）若函数f（x）=2x+b+2^x是“可拆函数”，求实数b的取值范围：
（3）证明：f（x）=cosx是“可拆函数”．

已知函数．
(Ⅰ)若，试判断在定义域内的单调性；
(Ⅱ) 当时，若在上有个零点，求的取值范围.

（本小题满分12分）
已知  
（1）求的值；
（2）当（其中，且为常数）时，是否存在最小值，如果存在求出最小值；如
果不存在，请说明理由；
（3）当时，求满足不等式的的范围.

已知函数，，的定义域为 
（1）求的值；
（2）若函数在区间上是单调递减函数，求实数的取值范围。

（本小题满分12分）函数是R上的偶函数，且当时，函数解析式为,
（Ⅰ）求的值；
（Ⅱ）求当时，函数的解析式。

星期天，刘先生到电信局打算上网开户，经询问，记录了可能需要的三种方式所花费的费用资料，现将资料整理如下：
1163普通：上网资费2元/小时；
2163A：每月50元（可上网50小时），超过50小时的部分资费2元/小时；
3ADSLD：每月70元，时长不限（其他因素忽略不计）.
请你用所学的函数知识对上网方式与费用问题作出研究：
（1）分别写出三种上网方式中所用资费与时间的函数解析式；
（2）在同一坐标系内分别画出三种方式所需资费与时间的函数图象；
（3）根据你的研究，请给刘先生一个合理化的建议.

已知是定义在上的奇函数，且，若时，有成立.
（1）判断在上的单调性，并证明；
（2）解不等式：；
（3）若当时，对所有的恒成立，求实数的取值范围.

设，（1）分别求；（2）然后归纳猜想一般性结论，并给出证明.

（本小题满分13分）已知函数（）在区间上有最大值和最小值．设．
(1）求、的值；
(2）若不等式在上有解，求实数的取值范围.

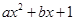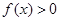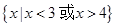已知函数，(1) 若的解集是，求实数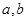的值；(2) 若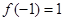且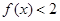恒成立，求实数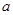的取值范围.

若定义在上的函数同时满足：①；②；③若，且，则成立.则称函数为“梦函数”.
（1）试验证在区间上是否为“梦函数”；
（2）若函数为“梦函数”，求的最值.

设，时，的最小值是-1，最大值是1，求、的值.

设 $a>0,b>0$，已知函数 $f\left(x\right)=\frac{ax+b}{x+1}$．
（Ⅰ）当 $a\ne b$时，讨论函数 $f\left(x\right)$的单调性；
（Ⅱ）当 $x>0$时，称 $f\left(x\right)$为 $a,b$关于 $x$的加权平均数．
（1）判断 $f\left(1\right),f\left(\sqrt{\frac{b}{a}}\right),f\left(\frac{b}{a}\right)$是否成等比数列，并证明 $f\left(\frac{b}{a}\right)\le f\left(\sqrt{\frac{b}{a}}\right)$；
（2） $a,b$的几何平均数记为 $G$．称 $\frac{2ab}{a+b}$为 $a,b$的调和平均数，记为 $H$．若 $H\le f\left(x\right)\le G$，求 $x$的取值范围．