高中数学函数迭代解答题

已知函数．
（1）解关于的不等式；
（2）若对，恒成立，求的取值范围．

有一个公益广告说：“若不注意节约用水，那么若干年后，最有一滴水只能是我们的眼泪。”我国是水资源匮乏的国家。为鼓励节约用水，某市打算出台一项水费政策措施，规定：每一季度每人用水量不超过5吨时，每吨水费收基本价1.3元；若超过5吨而不超过6吨时，超过部分的水费加收200%；若超过6吨而不超过7吨时，超过部分的水费加收400%。设某人本季度实际用水量为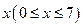吨，应交水费为f(x)，
（1）求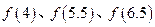的值；
（2）试求出函数f(x)的解析式。

函数在（-1，1）上是减函数，且为奇函数，满足
，试求的范围。

已知，，，比较与的大小。

已知函数有如下性质：如果常数，那么该函数在上是减函数，在上是增函数。
（1）如果函数在上是减函数，在上是增函数，求的值。
（2）设常数，求函数的最大值和最小值；

．(本小题满分14分)
设实数、同时满足条件：，且,
(1)求函数的解析式和定义域；
(2)判断函数的奇偶性；
(3)若方程恰有两个不同的实数根，求的取值范围

已知的图象过原点,且在点处的切线与轴平行.对任意,都有.
(1)求函数在点处切线的斜率;
(2)求的解析式;
(3)设,对任意,都有.求实数的取值范围

（本小题满分10分）设函数．
（Ⅰ）当时，求函数的定义域；
（Ⅱ）若函数的定义域为，试求实数的取值范围．

（满分12分）已知恒不为0，对于任意
等式恒成立.求证：是偶函数.

（本小题满分12分）
设p：实数x满足
（1）若为真，求实数x的取值范围；
（2）若p是q的充分不必要条件，求实数a的取值范围.

（本小题满分12分）(注意:在试题卷上作答无效)
已知函数.
(Ⅰ)若曲线在和处的切线互相平行，求的值；
(Ⅱ)求的单调区间；
(Ⅲ)设，若对任意，均存在，使得，求的取值范围.

已知函数是定义域为，且同时满足以下条件：
①在上是单调函数；
②存在闭区间（其中），使得当时，的取值集合也是．则称函数是“合一函数”．
（1）请你写出一个“合一函数”；
（2）若是“合一函数”，求实数的取值范围．
（注：本题求解中涉及的函数单调性不用证明，直接指出是增函数还是减函数即可）

已知函数f(x)＝log_a(x＋1)，g(x)＝2log_a(2x＋t)(t∈R)，其中x∈[0,15]，a＞0，且a≠1.
(1)若1是关于x的方程f(x)－g(x)＝0的一个解，求t的值；
(2)当0＜a＜1时，不等式f(x)≥g(x)恒成立，求t的取值范围；

（本小题满分16分）
已知函数＝＋，a≠0且a≠1．
（1）试就实数a的不同取值，写出该函数的单调增区间；
（2）已知当x＞0时，函数在(0，)上单调递减，在(，上单调递增，求a的值并写出函数的解析式；
（3）记（2）中的函数图象为曲线C，试问是否存在经过原点的直线l，使得l为曲线C的对称轴？若存在，求出直线l的方程；若不存在，请说明理由．

(本小题满分14分)
已知函数的极值点为和．
（Ⅰ）求实数，的值；
（Ⅱ）试讨论方程根的个数；
（Ⅲ）设，斜率为的直线与曲线交于
两点，试比较与的大小，并给予证明．