江苏省泰州市高三第二次模拟考试数学试卷
某高中共有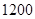 人,其中高一、高二、高三年级的人数依次成等差数列.现用分层抽样
人,其中高一、高二、高三年级的人数依次成等差数列.现用分层抽样
的方法从中抽取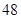 人,那么高二年级被抽取的人数为 .
人,那么高二年级被抽取的人数为 .
小明通过做游戏的方式来确定周末活动,他随机地往单位圆中投掷一点,若此点到圆心的距离大于 ,则周末看电影;若此点到圆心的距离小于
,则周末看电影;若此点到圆心的距离小于 ,则周末打篮球;否则就在家看书.那么小明周末在家看书的概率是 .
,则周末打篮球;否则就在家看书.那么小明周末在家看书的概率是 .
如图,矩形 所在平面与直角三角形
所在平面与直角三角形 所在平面互相垂直,
所在平面互相垂直, ,点
,点 分别是
分别是 的中点.
的中点.
(1)求证:  ∥平面
∥平面 ;
;
(2)求证:平面 平面
平面 .
.
如图,某市有一条东西走向的公路 ,现欲经过公路
,现欲经过公路 上的
上的 处铺设一条南北走向的公路
处铺设一条南北走向的公路 .在施工过程中发现在
.在施工过程中发现在 处的正北
处的正北 百米的
百米的 处有一汉代古迹.为了保护古迹,该市决定以
处有一汉代古迹.为了保护古迹,该市决定以 为圆心,
为圆心, 百米为半径设立一个圆形保护区.为了连通公路
百米为半径设立一个圆形保护区.为了连通公路 、
、 ,欲再新建一条公路
,欲再新建一条公路 ,点
,点 、
、 分别在公路
分别在公路 、
、 上,且要求
上,且要求 与圆
与圆 相切.
相切.
(1)当 距
距 处
处 百米时,求
百米时,求 的长;
的长;
(2)当公路 长最短时,求
长最短时,求 的长.
的长.
如图,在平面直角坐标系 中,椭圆
中,椭圆
 的左顶点为
的左顶点为 ,与
,与 轴平行的直线与椭圆
轴平行的直线与椭圆 交于
交于 、
、 两点,过
两点,过 、
、 两点且分别与直线
两点且分别与直线 、
、 垂直的直线相交于点
垂直的直线相交于点 .已知椭圆
.已知椭圆 的离心率为
的离心率为 ,右焦点到右准线的距离为
,右焦点到右准线的距离为 .
. 
(1)求椭圆 的标准方程;
的标准方程;
(2)证明点 在一条定直线上运动,并求出该直线的方程;
在一条定直线上运动,并求出该直线的方程;
(3)求 面积的最大值.
面积的最大值.
已知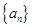 ,
,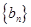 ,
, 都是各项不为零的数列,且满足
都是各项不为零的数列,且满足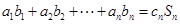 ,
,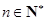 ,其中
,其中 是数列
是数列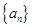 的前
的前 项和,
项和,  是公差为
是公差为 的等差数列.
的等差数列.
(1)若数列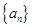 是常数列,
是常数列,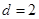 ,
,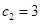 ,求数列
,求数列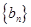 的通项公式;
的通项公式;
(2)若 (
( 是不为零的常数),求证:数列
是不为零的常数),求证:数列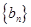 是等差数列;
是等差数列;
(3)若 (
(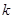 为常数,
为常数,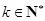 ),
),
 ,求证:对任意的
,求证:对任意的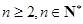 ,数列
,数列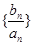 单调递减.
单调递减.
(本小题满分10分,几何证明选讲)
如图, 是圆
是圆 的切线,切点为
的切线,切点为 ,
, 是过圆心的割线且交圆
是过圆心的割线且交圆 于
于 点,过
点,过 作
作 的切线交
的切线交 于点
于点 .
.
求证:(1) ;(2)
;(2) .
.
(本小题满分10分,矩阵与变换)
已知矩阵 ,矩阵
,矩阵 ,直线
,直线 经矩阵
经矩阵 所对应的变换得到直线
所对应的变换得到直线 ,直线
,直线 又经矩阵
又经矩阵 所对应的变换得到直线
所对应的变换得到直线 .
.
(1)求 的值;(2)求直线
的值;(2)求直线 的方程.
的方程.
(本小题满分10分,坐标系与参数方程选讲)
已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的正半轴重合.若直线l的极坐标方程为 .
.
(1)把直线 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)已知 为椭圆
为椭圆 上一点,求
上一点,求 到直线
到直线 的距离的最小值.
的距离的最小值.
(本小题满分10分)某班组织的数学文化节活动中,通过抽奖产生了 名幸运之星.这
名幸运之星.这 名幸运之星可获得
名幸运之星可获得 、
、 两种奖品中的一种,并规定:每个人通过抛掷一枚质地均匀的骰子决定自己最终获得哪一种奖品,抛掷点数小于
两种奖品中的一种,并规定:每个人通过抛掷一枚质地均匀的骰子决定自己最终获得哪一种奖品,抛掷点数小于 的获得
的获得 奖品,抛掷点数不小于
奖品,抛掷点数不小于 的获得
的获得 奖品.
奖品.
(1)求这 名幸运之星中获得
名幸运之星中获得 奖品的人数大于获得
奖品的人数大于获得 奖品的人数的概率;
奖品的人数的概率;
(2)设 、
、 分别为获得
分别为获得 、
、 两种奖品的人数,并记
两种奖品的人数,并记 ,求随机变量
,求随机变量 的分布列及数学期望.
的分布列及数学期望.
 (
( 是虚数单位)是纯虚数,则实数
是虚数单位)是纯虚数,则实数 = .
= . ,
, ,若
,若 ,则
,则 .
. 的渐近线方程为
的渐近线方程为 ,则
,则 .
.
 ,则该圆柱的高为 .
,则该圆柱的高为 . 中,已知
中,已知 ,则
,则 .
. 的定义域为
的定义域为 ,值域为
,值域为 ,则实数
,则实数 的取值集合为 .
的取值集合为 . 满足
满足 ,则
,则 的取值范围是 .
的取值范围是 . 和
和 的图象在
的图象在 轴左、右两侧靠近
轴左、右两侧靠近 、
、 ,已知
,已知 为原点,则
为原点,则 .
. 的两条直线被圆
的两条直线被圆 :
: 所截得的弦长之比为
所截得的弦长之比为 ,则这两条直线的斜率之积为 .
,则这两条直线的斜率之积为 . 在区间
在区间 上单调递增,则实数
上单调递增,则实数 的取值范围是 .
的取值范围是 . 中,
中, 为边
为边 上一点,
上一点, ,若
,若 上,
上, .
. ,
, ,
, .
. ∥
∥ ,求角
,求角 的大小;
的大小; ,求
,求 的值.
的值. ,其中常数
,其中常数 .
. 时,求函数
时,求函数 的极值;
的极值; 有两个零点
有两个零点 ,求证:
,求证: ;
;  .
. 对于满足条件
对于满足条件 的任意实数
的任意实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. (
( ),
), 是关于
是关于 的
的 次多项式;
次多项式; 恒成立,求
恒成立,求 和
和 的值;并写出一个满足条件的
的值;并写出一个满足条件的 ,都存在与
,都存在与 ,
, ,
, ,…,
,…, ,
, .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号