(本小题满分10分)某班组织的数学文化节活动中,通过抽奖产生了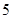 名幸运之星.这
名幸运之星.这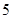 名幸运之星可获得
名幸运之星可获得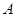 、
、 两种奖品中的一种,并规定:每个人通过抛掷一枚质地均匀的骰子决定自己最终获得哪一种奖品,抛掷点数小于
两种奖品中的一种,并规定:每个人通过抛掷一枚质地均匀的骰子决定自己最终获得哪一种奖品,抛掷点数小于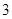 的获得
的获得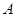 奖品,抛掷点数不小于
奖品,抛掷点数不小于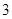 的获得
的获得 奖品.
奖品.
(1)求这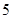 名幸运之星中获得
名幸运之星中获得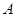 奖品的人数大于获得
奖品的人数大于获得 奖品的人数的概率;
奖品的人数的概率;
(2)设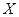 、
、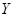 分别为获得
分别为获得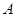 、
、 两种奖品的人数,并记
两种奖品的人数,并记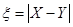 ,求随机变量
,求随机变量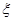 的分布列及数学期望.
的分布列及数学期望.
推荐套卷
(本小题满分10分)某班组织的数学文化节活动中,通过抽奖产生了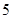 名幸运之星.这
名幸运之星.这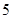 名幸运之星可获得
名幸运之星可获得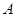 、
、 两种奖品中的一种,并规定:每个人通过抛掷一枚质地均匀的骰子决定自己最终获得哪一种奖品,抛掷点数小于
两种奖品中的一种,并规定:每个人通过抛掷一枚质地均匀的骰子决定自己最终获得哪一种奖品,抛掷点数小于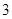 的获得
的获得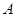 奖品,抛掷点数不小于
奖品,抛掷点数不小于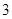 的获得
的获得 奖品.
奖品.
(1)求这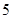 名幸运之星中获得
名幸运之星中获得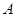 奖品的人数大于获得
奖品的人数大于获得 奖品的人数的概率;
奖品的人数的概率;
(2)设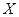 、
、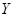 分别为获得
分别为获得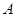 、
、 两种奖品的人数,并记
两种奖品的人数,并记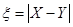 ,求随机变量
,求随机变量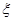 的分布列及数学期望.
的分布列及数学期望.