如图,某市有一条东西走向的公路 ,现欲经过公路
,现欲经过公路 上的
上的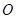 处铺设一条南北走向的公路
处铺设一条南北走向的公路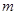 .在施工过程中发现在
.在施工过程中发现在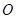 处的正北
处的正北 百米的
百米的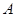 处有一汉代古迹.为了保护古迹,该市决定以
处有一汉代古迹.为了保护古迹,该市决定以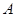 为圆心,
为圆心, 百米为半径设立一个圆形保护区.为了连通公路
百米为半径设立一个圆形保护区.为了连通公路 、
、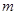 ,欲再新建一条公路
,欲再新建一条公路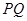 ,点
,点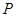 、
、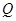 分别在公路
分别在公路 、
、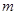 上,且要求
上,且要求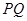 与圆
与圆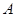 相切.
相切.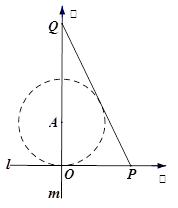
(1)当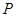 距
距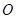 处
处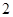 百米时,求
百米时,求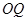 的长;
的长;
(2)当公路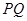 长最短时,求
长最短时,求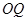 的长.
的长.
推荐套卷
如图,某市有一条东西走向的公路 ,现欲经过公路
,现欲经过公路 上的
上的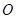 处铺设一条南北走向的公路
处铺设一条南北走向的公路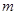 .在施工过程中发现在
.在施工过程中发现在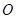 处的正北
处的正北 百米的
百米的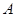 处有一汉代古迹.为了保护古迹,该市决定以
处有一汉代古迹.为了保护古迹,该市决定以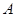 为圆心,
为圆心, 百米为半径设立一个圆形保护区.为了连通公路
百米为半径设立一个圆形保护区.为了连通公路 、
、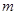 ,欲再新建一条公路
,欲再新建一条公路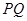 ,点
,点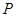 、
、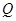 分别在公路
分别在公路 、
、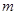 上,且要求
上,且要求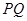 与圆
与圆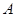 相切.
相切.
(1)当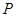 距
距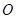 处
处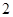 百米时,求
百米时,求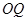 的长;
的长;
(2)当公路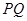 长最短时,求
长最短时,求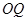 的长.
的长.