(本小题满分10分) 已知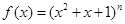 (
(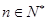 ),
),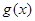 是关于
是关于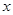 的
的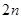 次多项式;
次多项式;
(1)若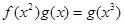 恒成立,求
恒成立,求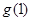 和
和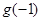 的值;并写出一个满足条件的
的值;并写出一个满足条件的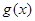 的表达式,无需证明.
的表达式,无需证明.
(2)求证:对于任意给定的正整数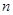 ,都存在与
,都存在与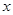 无关的常数
无关的常数 ,
,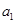 ,
,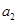 ,…,
,…,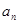 ,
,
使得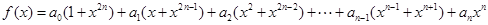 .
.
相关知识点
推荐套卷
(本小题满分10分) 已知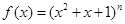 (
(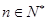 ),
),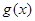 是关于
是关于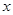 的
的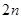 次多项式;
次多项式;
(1)若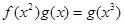 恒成立,求
恒成立,求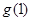 和
和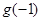 的值;并写出一个满足条件的
的值;并写出一个满足条件的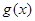 的表达式,无需证明.
的表达式,无需证明.
(2)求证:对于任意给定的正整数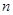 ,都存在与
,都存在与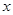 无关的常数
无关的常数 ,
,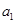 ,
,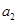 ,…,
,…,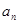 ,
,
使得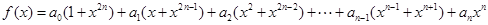 .
.