(本小题满分12分)设函数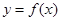 在
在 上的导函数为
上的导函数为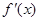 ,
,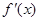 在
在 上的导函数为
上的导函数为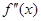 ,若在
,若在 上,
上,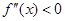 恒成立,则称函数
恒成立,则称函数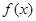 在
在 上为“凸函数”.已知
上为“凸函数”.已知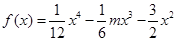 .
.
(1)若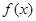 为区间
为区间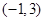 上的“凸函数”,试确定实数
上的“凸函数”,试确定实数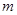 的值;
的值;
(2)若当实数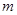 满足
满足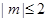 时,函数
时,函数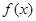 在
在 上总为“凸函数”,求
上总为“凸函数”,求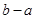 的最大值.
的最大值.
相关知识点
推荐套卷
(本小题满分12分)设函数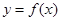 在
在 上的导函数为
上的导函数为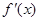 ,
,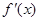 在
在 上的导函数为
上的导函数为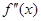 ,若在
,若在 上,
上,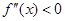 恒成立,则称函数
恒成立,则称函数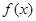 在
在 上为“凸函数”.已知
上为“凸函数”.已知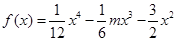 .
.
(1)若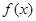 为区间
为区间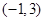 上的“凸函数”,试确定实数
上的“凸函数”,试确定实数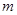 的值;
的值;
(2)若当实数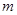 满足
满足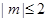 时,函数
时,函数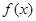 在
在 上总为“凸函数”,求
上总为“凸函数”,求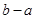 的最大值.
的最大值.