给定函数 和常数
和常数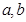 ,若
,若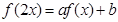 恒成立,则称
恒成立,则称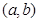 为函数
为函数 的一个“好数对”;若
的一个“好数对”;若 恒成立,则称
恒成立,则称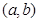 为函数
为函数 的一个“类好数对”.已知函数
的一个“类好数对”.已知函数 的定义域为
的定义域为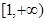 .
.
(Ⅰ)若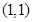 是函数
是函数 的一个“好数对”,且
的一个“好数对”,且 ,求
,求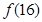 ;
;
(Ⅱ)若 是函数
是函数 的一个“好数对”,且当
的一个“好数对”,且当 时,
时, ,求证:
,求证:
函数 在区间
在区间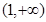 上无零点;
上无零点;
(Ⅲ)若 是函数
是函数 的一个“类好数对”,
的一个“类好数对”, ,且函数
,且函数 单调递增,比较
单调递增,比较 与
与 的大小,并说明理由.
的大小,并说明理由.
相关知识点
推荐套卷
给定函数 和常数
和常数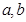 ,若
,若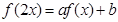 恒成立,则称
恒成立,则称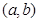 为函数
为函数 的一个“好数对”;若
的一个“好数对”;若 恒成立,则称
恒成立,则称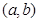 为函数
为函数 的一个“类好数对”.已知函数
的一个“类好数对”.已知函数 的定义域为
的定义域为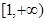 .
.
(Ⅰ)若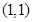 是函数
是函数 的一个“好数对”,且
的一个“好数对”,且 ,求
,求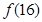 ;
;
(Ⅱ)若 是函数
是函数 的一个“好数对”,且当
的一个“好数对”,且当 时,
时, ,求证:
,求证:
函数 在区间
在区间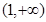 上无零点;
上无零点;
(Ⅲ)若 是函数
是函数 的一个“类好数对”,
的一个“类好数对”, ,且函数
,且函数 单调递增,比较
单调递增,比较 与
与 的大小,并说明理由.
的大小,并说明理由.