在△ABC中，顶点A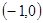
，B
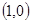，动点D，E满足：①
；②
，③
共线.
（Ⅰ）求△ABC顶点C的轨迹方程；
（Ⅱ）是否存在圆心在原点的圆，只要该圆的切线与顶点C的轨迹有两个不同交点M，N，就一定有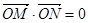
，若存在，求该圆的方程；若不存在，请说明理由.
相关试题
，
，求
；
的最大值。
，
，
，
的值；（2）求
的值。
．
的解集为
，求实数a的值；
使
成立，求实数
的取值范围．
，求
中
的最大值和最小值.
中，AB=AC，过点A的直线与其外接圆交于点P，交BC延长线于点D。
；
的值。推荐套卷
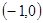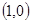在△ABC中，顶点A，B，动点D，E满足：①；②，③共线.
（Ⅰ）求△ABC顶点C的轨迹方程；
（Ⅱ）是否存在圆心在原点的圆，只要该圆的切线与顶点C的轨迹有两个不同交点M，N，就一定有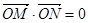，若存在，求该圆的方程；若不存在，请说明理由.
粤公网安备 44130202000953号