设数列{an}为前n项和为Sn，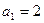
，数列{ Sn +2}是以2为公比的等比数列．
(1)求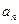
；
(2)抽去数列{an}中的第1项，第4项，第7项，……，第3n-2项，余下的项顺序不变，组成一个新数列{cn}，若{cn}的前n项和为Tn，求证：
＜≤
相关试题
满足
,求
的最小值有如下解法：
且
.
. 
.
中, ∠A,∠B,∠C， 的对边分别是a, b, c，则求满足下列条件的∠B的范围分别是什么。
。相关知识点
推荐套卷
设数列{an}为前n项和为Sn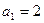，，数列{ Sn +2}是以2为公比的等比数列．
(1)求；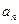
(2)抽去数列{an}中的第1项，第4项，第7项，……，第3n-2项，余下的项顺序不变，组成一个新数列{cn}，若{cn}的前n项和为Tn，求证：
＜≤
粤公网安备 44130202000953号