（本小题满分12
分）
设函数f(x)的定义域为R，若|f(x)|≤|x|对任意的实数x均成立，则称函数f(x)为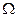
函数。
（1）试判断函数
=
=
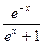中哪些是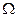函数，并说明理由；
（2）求证：若a>1，则函数f(x)=ln(x2+a)-lna是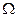函数。
相关试题
n2+
n，试求出数列{|an|}的前n项和Tn．
+
+
+…+
的值为多少？
n2+
n，求数列{an}的通项公式．相关知识点
推荐套卷
（本小题满分12分）
设函数f(x)的定义域为R，若|f(x)|≤|x|对任意的实数x均成立，则称函数f(x)为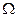函数。
（1）试判断函数= =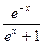中哪些是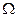函数，并说明理由；
（2）求证：若a>1，则函数f(x)=ln(x2+a)-lna是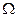函数。
粤公网安备 44130202000953号