已知函数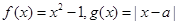 .
.
(1)当 时,求
时,求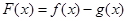 的零点;
的零点;
(2)若方程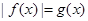 有三个不同的实数解,求
有三个不同的实数解,求 的值;
的值;
(3)求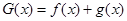 在
在 上的最小值
上的最小值 .[来
.[来
给定函数 和常数
和常数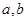 ,若
,若 恒成立,则称
恒成立,则称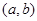 为函数
为函数 的一个“好数对”;若
的一个“好数对”;若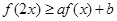 恒成立,则称
恒成立,则称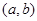 为函数
为函数 的一个“类好数对”.已知函数
的一个“类好数对”.已知函数 的定义域为
的定义域为 .
.
(1)若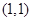 是函数
是函数 的一个“好数对”,且
的一个“好数对”,且 ,求
,求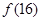 ;
;
(2)若 是函数
是函数 的一个“好数对”,且当
的一个“好数对”,且当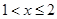 时,
时,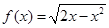 ,求证:
,求证:
函数 在区间
在区间 上无零点;
上无零点;
(3)若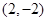 是函数
是函数 的一个“类好数对”,
的一个“类好数对”, ,且函数
,且函数 单调递增,比较
单调递增,比较 与
与 的大小,并说明理由.
的大小,并说明理由.
(本小题满分14分)已知命题p:方程x2+mx+1=0有两个不相等的实根;q:不等式4x2+4(m–2)x+1>0的解集为R.
(1)若命题q为真,求实数m的取值范围.
(2)若命题“p且q”和“非p”为假,求实数m的取值范围
(本小题满分13分)已知函数 .
.
(Ⅰ)当 时,函数
时,函数 恰有3个零点,求实数
恰有3个零点,求实数 的取值范围;
的取值范围;
(Ⅱ)若对任意 ,有
,有 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知 在
在 时有极值0。
时有极值0。
(1)求常数 a,b的值;
(2)求f(x)的单调区间。
(3)方程f(x)=c在区间[-4,0]上有三个不同的实根时实数 的范围。
的范围。
已知函数f(x)= 和函数g(x)=x|x﹣m|+2m﹣8,其中m为参数,且满足m≤5.
和函数g(x)=x|x﹣m|+2m﹣8,其中m为参数,且满足m≤5.
(1)若m=2,写出函数g(x)的单调区间(无需证明);
(2)若方程f(x)= 在x∈[﹣2,+∞)上有唯一解,求实数m的取值范围;
在x∈[﹣2,+∞)上有唯一解,求实数m的取值范围;
(3)若对任意x1∈[4,+∞),存在x2∈(﹣∞,4],使得f(x2)=g(x1)成立,求实数m的取值范围.