已知函数 .
.
(1)若函数 在区间[-1,1]上存在零点,求实数a的取值范围;
在区间[-1,1]上存在零点,求实数a的取值范围;
(2)当a=0时,若对任意的 ,总存在
,总存在 ,使
,使 成立,求实数m的取值范围.
成立,求实数m的取值范围.
给定函数 和常数
和常数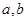 ,若
,若 恒成立,则称
恒成立,则称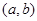 为函数
为函数 的一个“好数对”;若
的一个“好数对”;若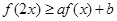 恒成立,则称
恒成立,则称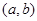 为函数
为函数 的一个“类好数对”.已知函数
的一个“类好数对”.已知函数 的定义域为
的定义域为 .
.
(1)若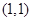 是函数
是函数 的一个“好数对”,且
的一个“好数对”,且 ,求
,求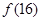 ;
;
(2)若 是函数
是函数 的一个“好数对”,且当
的一个“好数对”,且当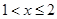 时,
时,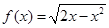 ,求证:
,求证:
函数 在区间
在区间 上无零点;
上无零点;
(3)若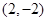 是函数
是函数 的一个“类好数对”,
的一个“类好数对”, ,且函数
,且函数 单调递增,比较
单调递增,比较 与
与 的大小,并说明理由.
的大小,并说明理由.
设二次函数 ,函数
,函数 的两个零点为m,n(m<n).
的两个零点为m,n(m<n).
(1)若m=-1,n=2,求不等式F(x)>0的解集;
(2)若a>0,且 ,比较f(x)与m的大小.
,比较f(x)与m的大小.
(本小题满分16分)已知函数 (
( 是不同时为零的常数),导函数为
是不同时为零的常数),导函数为 .
.
(1)当 时,若存在
时,若存在 ,使得
,使得 成立,求
成立,求 的取值范围;
的取值范围;
(2)求证:函数 在
在 内至少有一个零点;
内至少有一个零点;
(3)若函数 为奇函数,且在
为奇函数,且在 处的切线垂直于直线
处的切线垂直于直线 ,关于
,关于 的方程
的方程 ,在
,在 上有且只有一个实数根,求实数
上有且只有一个实数根,求实数 的取值范围.
的取值范围.
(本小题满分16分)已知 为
为 上的奇函数,当
上的奇函数,当 时,
时, 为二次函数,且满足
为二次函数,且满足 ,不等式组
,不等式组 的解集是
的解集是 .
.
(1)求函数 的解析式;
的解析式;
(2)作出 的图象并根据图象讨论关于
的图象并根据图象讨论关于 的方程:
的方程:
 根的个数.
根的个数.
(本小题满分14分)已知
(1)求 ,
, ;
;
(2)画出 的图像;
的图像;
(3)若 ,问
,问 为何值时,方程没有根?有一个根?两个根?
为何值时,方程没有根?有一个根?两个根?

(本小题满分14分)已知命题p:方程x2+mx+1=0有两个不相等的实根;q:不等式4x2+4(m–2)x+1>0的解集为R.
(1)若命题q为真,求实数m的取值范围.
(2)若命题“p且q”和“非p”为假,求实数m的取值范围
已知 在
在 时有极值0。
时有极值0。
(1)求常数 a,b的值;
(2)求f(x)的单调区间。
(3)方程f(x)=c在区间[-4,0]上有三个不同的实根时实数 的范围。
的范围。
(本小题满分13分)已知函数 .
.
(Ⅰ)当 时,函数
时,函数 恰有3个零点,求实数
恰有3个零点,求实数 的取值范围;
的取值范围;
(Ⅱ)若对任意 ,有
,有 恒成立,求
恒成立,求 的取值范围.
的取值范围.