高中数学不定方程和方程组解答题

设函数 $f\left(x\right)=x^3+2a{x}^2+bx+a,g\left(x\right)=x^2-3x+2$，其中 $x\in R$， $a,b$为常数，已知曲线 $y=f\left(x\right)$与 $y=g\left(x\right)$在点 $(2,0)$处有相同的切线 $l$．
（Ⅰ）求 $a,b$的值，并写出切线 $l$的方程；
（Ⅱ）若方程 $f\left(x\right)+g\left(x\right)=mx$有三个互不相同的实根 $0,x_1,x_2$，其中 $x_1<x_2$，且对任意的 $x\in [x_1,x_2],f\left(x\right)+g\left(x\right)<m(x-1)$恒成立，求实数 $m$的取值范围．

已知函数
（1）若函数在上无零点，请你探究函数在上的单调性；
（2）设，若对任意的，恒有成立，求实数的取值范围．

已知函数，其中.
（1）若，求函数的定义域和极值；
（2）当时，试确定函数的零点个数，并证明.

（本小题满分14分）已知函数，其中
（1）若在区间上有零点，求实数的取值范围；
（2）设函数，是否存在实数，对任意给定的非零实数，存在唯一的非零实数，使得？若存在，求出的值，若不存在，请说明理由．

设函数中，为奇数，均为整数，且均为奇数.求证：无整数根。

已知函数f（x）=a（x+）﹣|x﹣|（x＞0）a∈R．
（1）若a=，求y=f（x）的单调区间；
（2）若关于x的方程f（x）=t有四个不同的解x₁，x₂，x₃，x₄，求实数a，t应满足的条件；
（3）在（2）条件下，若x₁，x₂，x₃，x₄成等比数列，求t用a表示．

设函数，.
（1）解方程：；
（2）令，，求证：

（3）若是实数集上的奇函数，且对任意实数恒成立，求实数的取值范围.

（本题满分14分，第1小题6分，第2小题8分）
已知函数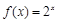的反函数为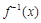
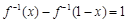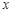（1）若，求实数的值；
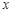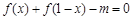（2）若关于的方程在区间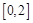内有解，求实数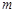的取值范围；

已知函数．
（1）当时，写出的单调区间；
（2）当时，求的最小值；
（3）试讨论关于的方程的解的个数．

已知函数f（x）=，若存在实数a，b，c，d，满足f（a）=f（b）=f（c）=f（d），其中0＜a＜b＜c＜d，则abcd的取值范围      ．

已知函数.
（1）当时，求函数的零点；
（2）若函数有零点，求实数a的取值范围.

已知函数的定义域为[2,3]，值域为[1,4]；设．
（1）求a，b的值；
（2）若不等式在上恒成立，求实数k的取值范围；
（3）若有三个不同的实数解，求实数k的取值范围．

已知函数（）．
（1）若函数有两个零点，求的取值范围；
（2）若函数在区间与上各有一个零点，求的取值范围．

（本小题满分12分）已知函数，（）．
（Ⅰ）求函数的递增区间；
（Ⅱ）若函数在上有两个不同的零点、，求的值．

设关于的方程有两个实根，函数.
（1）求的值；
（2）判断在区间的单调性，并加以证明；
（3）若均为正实数，证明：