高中数学不定方程和方程组解答题

4-5：不等式选讲（本小题满分10分）
已知函数．
（1）若是定义域为的奇函数，试求实数的值；
（2）在（1）的条件下，若函数有三个零点，试求实数的取值范围．

设命题：方程无实数根；命题：函数的定义域是．如果命题为真命题，求实数的取值范围．

已知函数，设方程有两个实数根
（1）若果，设函数的对称轴为，求证：
（2）如果的两个实数根相差2，求实数b的取值范围。

已知函数，设方程有两个实数根
（1）若果，设函数的对称轴为，求证：
（2）如果的两个实数根相差2，求实数b的取值范围。

已知函数在处取得极值为.
（1）求实数的值；
（2）若关于的方程在有两个不同的解，求实数的取值范围.

设函数．
（1）求函数的单调区间.
（2）若方程有且仅有三个实根，求实数的取值范围.

已知命题方程有两个不等的正实数根；命题方程无实数根。若“或”为真命题，求的取值范围.

设函数．
（1）求函数的单调区间．
（2）若方程有且仅有三个实根，求实数的取值范围．

已知，函数．
（Ⅰ）当时，求函数的最小值；
（Ⅱ）讨论的图象与的图象的公共点个数．

设函数
（Ⅰ）当时，讨论函数f(x)的零点个数；
（Ⅱ）若对于给定的实数，存在实数，对于任意实数，都有不等式恒成立，求实数的取值范围。

设函数.
（Ⅰ）当时，讨论函数的零点个数；
（Ⅱ）若对于给定的实数，存在实数，使不等式对于任意恒成立。试将最大实数表示为关于的函数，并求的取值范围.

（本小题满分14分）已知为实数，对于实数和，定义运算“”：，
设．
（Ⅰ）若在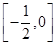上为增函数，求实数的取值范围；
（Ⅱ）若方程有三个不同的解，记此三个解的积为，求的取值范围．

设，.
（Ⅰ）若在上有两个不等实根，求的取值范围；
（Ⅱ）若存在，使得对任意的，都有成立，求实数的取值范围.

已知函数，其中，是自然对数的底数若，且函数在区间内有零点，求实数的取值范围．

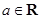已知,函数．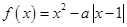
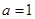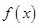（Ⅰ）当时,求函数的最小值；
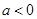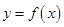（Ⅱ）当时,讨论的图象与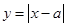的图象的公共点个数．