(本小题满分13 分)已知函数 .
.
(Ⅰ)若函数 在定义域内单调递增,求实数a的取值范围;
在定义域内单调递增,求实数a的取值范围;
(Ⅱ)若 ,且关于x的方程
,且关于x的方程 在
在 上恰有两个不等的实根,求实数b的取值范围;
上恰有两个不等的实根,求实数b的取值范围;
(Ⅲ)设各项为正数的数列 满足
满足 ,
,
求证: .
.
已知函数 是定义在
是定义在 上的奇函数.当
上的奇函数.当 时,
时, ,且图象过点
,且图象过点 与点
与点 .
.
(Ⅰ)求实数 的值,并求函数
的值,并求函数 的解析式;
的解析式;
(Ⅱ)若关于 的方程
的方程 有两个不同的实数解,请写出实数
有两个不同的实数解,请写出实数 的取值范围;
的取值范围;
(Ⅲ)解关于 的不等式
的不等式 ,写出解集.
,写出解集.
【原创】设命题p:直线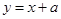 与圆
与圆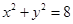 有公共点,命题q:关于
有公共点,命题q:关于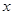 的方程
的方程
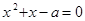 的一根大于1,另一根小于1,命题“
的一根大于1,另一根小于1,命题“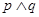 ”为假命题,命题“
”为假命题,命题“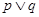 ”为真命题,求实数
”为真命题,求实数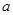 的取值范围.
的取值范围.
已知函数 .
.
(1)当 时,求
时,求 的单调减区间;
的单调减区间;
(2)若方程 恰好有一个正根和一个负根,求实数
恰好有一个正根和一个负根,求实数 的最大值.
的最大值.
(本小题满分14分)已知 为常数,且
为常数,且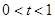 ,函数
,函数 的最小值和函数
的最小值和函数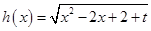 的最小值都是函数
的最小值都是函数
 R
R 的零点.
的零点.
(1)用含 的式子表示
的式子表示 ,并求出
,并求出 的取值范围;
的取值范围;
(2)求函数 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
已知函数 ,
, .
.
(1)证明:函数 在区间
在区间 上为增函数,并指出函数
上为增函数,并指出函数 在区间
在区间 上的单调性.
上的单调性.
(2)若函数 的图像与直线
的图像与直线 有两个不同的交点
有两个不同的交点 ,
, ,其中
,其中 ,求
,求 关于
关于 的函数关系式.
的函数关系式.
(3)求 的取值范围.
的取值范围.
已知函数
(1)若 在区间[1,+∞)上是增函数,求实数a的取值范围;
在区间[1,+∞)上是增函数,求实数a的取值范围;
(2)若x=- 是
是 的极值点,求
的极值点,求 在[1,a]上的最大值;
在[1,a]上的最大值;
(3)在(2)的条件下,是否存在实数b,使得函数 =bx的图象与函数
=bx的图象与函数 的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
(本题满分12分)已知函数f(x)= (
( ).
).
(1)求函数f(x)的周期和递增区间;
(2)若函数 在[0,
在[0, ]上有两个不同的零点x1、x2,求tan(x1+x2)的值.
]上有两个不同的零点x1、x2,求tan(x1+x2)的值.
(本小题满分9分)设命题 方程
方程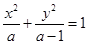 表示双曲线,命题
表示双曲线,命题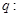 函数
函数 有两个不同的零点,如果“
有两个不同的零点,如果“ ”为真,且“
”为真,且“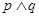 ”为假,求
”为假,求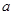 的取值范围.
的取值范围.