已知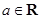 ,函数
,函数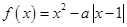 .
.
(Ⅰ)当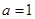 时,求函数
时,求函数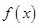 的最小值;
的最小值;
(Ⅱ)当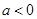 时,讨论
时,讨论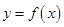 的图象与
的图象与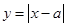 的图象的公共点个数.
的图象的公共点个数.
定义在 上的函数
上的函数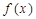 ,如果满足:对任意
,如果满足:对任意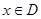 ,存在常数
,存在常数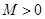 ,都有
,都有
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中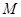 称为函数
称为函数 的上界.已知函数
的上界.已知函数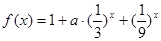 ,
,
(1)当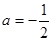 时,求函数
时,求函数 在
在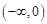 上的值域,并判断函数
上的值域,并判断函数 在
在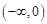 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数 在
在 上是以4为上界的有界函数,求实数
上是以4为上界的有界函数,求实数 的取值范围;
的取值范围;
记方程①:
,方程②:
,方程③:
,其中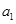 ,
, ,
, 是正实数.当
,
,
成等比数列时,下列选项中,能推出方程③无实根的是()
是正实数.当
,
,
成等比数列时,下列选项中,能推出方程③无实根的是()
| A. | 方程①有实根,且②有实根 | B. | 方程①有实根,且②无实根 |
| C. | 方程①无实根,且②有实根 | D. | 方程①无实根,且②无实根 |
设 .
(Ⅰ)求
;
(Ⅱ)证明:
在
内有且仅有一个零点(记为
),且
.