已知 ,函数
,函数 .
.
(Ⅰ)当 时,求函数
时,求函数 的最小值;
的最小值;
(Ⅱ)讨论 的图象与
的图象与 的图象的公共点个数.
的图象的公共点个数.
已知定义在 上的函数
上的函数 满足:
满足:
① ;
;
② ;
;
③当 时,
时,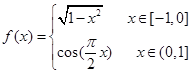 ;
;
则函数 在区间
在区间 上的零点个数为
上的零点个数为
| A.5 | B.6 | C.7 | D.8 |
设函数
(Ⅰ)当 时,讨论函数f(x)的零点个数;
时,讨论函数f(x)的零点个数;
(Ⅱ)若对于给定的实数 ,存在实数
,存在实数 ,对于任意实数
,对于任意实数 ,都有不等式
,都有不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
设函数 .
.
(Ⅰ)当 时,讨论函数
时,讨论函数 的零点个数;
的零点个数;
(Ⅱ)若对于给定的实数 ,存在实数
,存在实数 ,使不等式
,使不等式 对于任意
对于任意 恒成立。试将最大实数
恒成立。试将最大实数 表示为关于
表示为关于 的函数
的函数 ,并求
,并求 的取值范围.
的取值范围.
已知 则
则 ;若关于x的方程f(x)=ax+1恰有三个不同的解,则实数a的取值范围为 .
;若关于x的方程f(x)=ax+1恰有三个不同的解,则实数a的取值范围为 .
(本小题满分14分)已知 为实数,对于实数
为实数,对于实数 和
和 ,定义运算“
,定义运算“ ”:
”: ,
,
设 .
.
(Ⅰ)若 在
在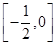 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)若方程 有三个不同的解,记此三个解的积为
有三个不同的解,记此三个解的积为 ,求
,求 的取值范围.
的取值范围.
若过点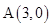 的直线
的直线 与圆
与圆 有公共点,则直线
有公共点,则直线 斜率的取值范围为( )
斜率的取值范围为( )
A.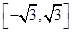 |
B. |
C. |
D. |